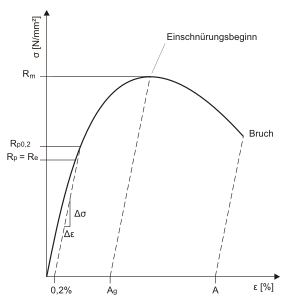
Spannungs-Dehnungs-Diagramm

In der Technik ist es häufig von großer Bedeutung, die Eigenschaften eines verwendeten Materials hinsichtlich seiner Festigkeit, seiner Plastizität bzw. seiner Sprödigkeit, seiner Elastizität und einiger anderer Eigenschaften genau zu kennen. ⓘ

Zu diesem Zweck werden Materialproben im Zugversuch getestet, indem die Probe mit bekanntem Ausgangsquerschnitt in eine Zugprüfmaschine eingespannt und mit einer Zugkraft F belastet wird. ⓘ

Unter Erhöhung der Kraft wird diese dann über der verursachten Längenänderung ΔL grafisch dargestellt. Diese Kurve bezeichnet man als Kraft-Verlängerungs-Diagramm. ⓘ

Um eine Messkurve zu erhalten, die nur von der Art und Struktur des geprüften Materials, also nicht von den geometrischen Abmessungen der Probe abhängt, verwendet man reduzierte Einheiten, das heißt die Längenänderung ΔL wird auf die Anfangslänge L₀ und die Kraft F auf den senkrechten Querschnitt S₀ des Körpers im undeformierten Zustand bezogen. ⓘ

Diese jetzt von der Probenform unabhängige Kurve nennt man Spannungs-Dehnungs-Diagramm. ⓘ

Dehnung:

$\varepsilon ={\frac {\Delta L}{L_{0}}}$ ⓘ

(Nenn-)Spannung:

$\sigma ={\frac {F}{S_{0}}}$ ⓘ

Die Dehnung ist eine Größe der Dimension Zahl. Häufig wird sie in Prozent oder in Promille angegeben (z. B. „0,2-%-Dehngrenze“).
Die Einheit der Spannung ist N/m² (= 1 Pa). Im Maschinenbau und der Werkstoffkunde wird oft mit der Einheit 1 N/mm² (= 1 MPa) gearbeitet. ⓘ

Je nachdem, ob man den Versuch spannungsgeregelt oder dehnungsgeregelt fährt, ist die Spannung bzw. die Dehnung die unabhängige Variable. Es hat sich jedoch eingebürgert, immer die Spannung über der Dehnung aufzutragen. ⓘ

Die (technische) Spannung bezieht sich immer auf den Ausgangsquerschnitt $S_{0}$. Die wahre Spannung steigt jedoch im Zugversuch ab $R_{\mathrm {m} }$ weiter an, da sich die Querschnittsfläche aufgrund von Einschnürung verringert. Die wahre Spannung kann allerdings nicht direkt mit dem Zugversuch ermittelt werden, daher verwendet man fast immer die technische Spannung $\sigma$. Eine Möglichkeit, die wahre Spannung zu ermitteln, ist die gleichzeitige optische Auswertung. Die technische Spannung und Dehnung kann in Näherung auch in die wahre Spannung und Dehnung umgerechnet werden: Wahre Spannung:

$\sigma _{W}=\sigma \cdot (1+\varepsilon )$

Wahre Dehnung:

$\varepsilon _{W}=\int _{l_{0}}^{l}{\frac {\mathrm {d} l}{l}}=\ln(1+\varepsilon )$ ⓘ

Man unterscheidet verschiedene Bereiche im Spannungs-Dehnungs-Diagramm:

• den linear-elastischen Bereich (Proportionalbereich, „Hookesche Gerade“), in welchem die Dehnung der Spannung proportional ist und somit das Hookesche Gesetz gilt
• den nichtlinear-elastischen Bereich, in welchem die Verformung noch reversibel ist (elastisch) aber nicht mehr der Spannung proportional ist.
• den elastisch-plastischen Bereich, in welchem die Verformung teilweise plastisch – das heißt irreversibel – ist. Wenn die Elastizitätsgrenze überschritten wird, entstehen im Bauteil bleibende Deformationen aufgrund von Versetzungsbewegungen, die temperatur- und dehnratenabhängig sind (Thermisch aktiviertes Fließen).

Baustähle zeigen einen ausgeprägten Streckgrenzeneffekt, der durch interstitiell eingelagerte Fremdatome, beispielsweise Kohlen- und Stickstoff hervorgerufen wird. ⓘ

• 

  Abb. 1 schematisches Spannungs-Dehnungs-Diagramm mit ausgeprägter Streckgrenze

• 

  Abb. 2 schematisches Spannungs-Dehnungs-Diagramm mit kontinuierlichem Fließbeginn und eingetragener 0,2-%-Dehngrenze

• 

  Abb. 3 schematisches Feindehnungsdiagramm ⓘ

In den Diagrammen sind folgende Abkürzungen verwendet worden:

• $R_{\mathrm {m} }$ = Zugfestigkeit
• $R_{\mathrm {eH} }$ = obere Streckgrenze
• $R_{\mathrm {eL} }$ = untere Streckgrenze
• $R_{\mathrm {p0,2} }$ = Dehngrenze mit 0,2 % plastischer Verformung
• $E$ = Elastizitätsmodul
• $A$ = Bruchdehnung
• $A_{\mathrm {g} }$ = Gleichmaßdehnung
• $A_{\mathrm {L} }$ = Lüdersdehnung ⓘ

In den Ingenieur- und Werkstoffwissenschaften gibt die Spannungs-Dehnungskurve eines Materials das Verhältnis zwischen Spannung und Dehnung an. Sie wird durch schrittweises Aufbringen einer Last auf einen Prüfkörper und Messen der Verformung ermittelt, woraus sich die Spannung und Dehnung bestimmen lassen (siehe Zugversuch). Diese Kurven geben Aufschluss über viele Eigenschaften eines Materials, wie z. B. den Elastizitätsmodul, die Streckgrenze und die Höchstzugfestigkeit. ⓘ

Definition

Im Allgemeinen können Kurven, die das Verhältnis zwischen Spannung und Dehnung bei jeder Form der Verformung darstellen, als Spannungs-Dehnungs-Kurven bezeichnet werden. Die Spannung und die Dehnung können normal, scher oder gemischt sein, sie können auch einachsig, zweiachsig oder mehrachsig sein und sich sogar mit der Zeit ändern. Die Form der Verformung kann Kompression, Dehnung, Torsion, Rotation usw. sein. Wenn nicht anders angegeben, bezieht sich die Spannungs-Dehnungskurve auf das Verhältnis zwischen der axialen Normalspannung und der axialen Normaldehnung von Materialien, die in einem Zugversuch gemessen werden. ⓘ

Technische Spannung und Dehnung

Nehmen wir an, ein Stab mit ursprünglichem Querschnitt $A_{0}$ auf den gleiche und entgegengesetzte Kräfte einwirken $F$ die an den Enden ziehen, so dass der Stab unter Spannung steht. Das Material erfährt eine Spannung, die als Verhältnis zwischen der Kraft und der Querschnittsfläche des Stabes definiert ist, sowie eine axiale Dehnung:

$\sigma ={\tfrac {F}{A_{0}}}$

$\varepsilon ={\tfrac {L-L_{0}}{L_{0}}}={\tfrac {\Delta L}{L_{0}}}$ ⓘ

Der Index 0 steht für die ursprünglichen Abmessungen der Probe. Die SI-Einheit für die Spannung ist Newton pro Quadratmeter oder Pascal (1 Pascal = 1 Pa = 1 N/m²), die Dehnung ist einheitenlos. Die Spannungs-Dehnungskurve für dieses Material wird aufgezeichnet, indem die Probe gedehnt und die Spannungsänderung mit der Dehnung aufgezeichnet wird, bis die Probe bricht. Vereinbarungsgemäß wird die Dehnung auf die horizontale Achse und die Spannung auf die vertikale Achse gesetzt. Für technische Zwecke wird häufig angenommen, dass sich die Querschnittsfläche des Materials während des gesamten Verformungsprozesses nicht ändert. Dies ist jedoch nicht der Fall, da die tatsächliche Fläche während der Verformung aufgrund elastischer und plastischer Verformung abnimmt. Die Kurve, die auf dem ursprünglichen Querschnitt und der Messlänge basiert, wird als technische Spannungs-Dehnungskurve bezeichnet, während die Kurve, die auf der momentanen Querschnittsfläche und -länge basiert, als wahre Spannungs-Dehnungskurve bezeichnet wird. Sofern nicht anders angegeben, wird im Allgemeinen die technische Spannungs-Dehnungs-Kurve verwendet. ⓘ

Echte Spannung und Dehnung

Der Unterschied zwischen echter Spannungs-Dehnungs-Kurve und technischer Spannungs-Dehnungs-Kurve ⓘ

Aufgrund der Schrumpfung der Querschnittsfläche und der Vernachlässigung der Auswirkung der entwickelten Dehnung auf die weitere Dehnung unterscheiden sich die wahren Spannungen und Dehnungen von den technischen Spannungen und Dehnungen. ⓘ

$\sigma _{\text{t}}={\tfrac {F}{A}}$

$\varepsilon _{\text{t}}=\int {\tfrac {\delta L}{L}}$ ⓘ

Hier sind die Abmessungen Momentanwerte. Es wird angenommen, dass das Volumen der Probe erhalten bleibt und die Verformung gleichmäßig erfolgt, ⓘ

$A_{0}L_{0}=AL$ ⓘ

Die wahre Spannung und Dehnung kann durch die technische Spannung und Dehnung ausgedrückt werden. Für die wahre Spannung, ⓘ

$\sigma _{\text{t}}={\tfrac {F}{A}}={\tfrac {F}{A_{0}}}{\tfrac {A_{0}}{A}}={\tfrac {F}{A_{0}}}{\tfrac {L}{L_{0}}}=\sigma (1+\varepsilon )$ ⓘ

Für die Dehnung, ⓘ

$\delta \varepsilon _{\text{t}}={\tfrac {\delta L}{L}}$ ⓘ

Integrieren Sie beide Seiten und wenden Sie die Randbedingung an, ⓘ

$\varepsilon _{\text{t}}=\ln \left({\tfrac {L}{L_{0}}}\right)=\ln(1+\varepsilon )$ ⓘ

Bei einem Zugversuch ist also die wahre Spannung größer als die technische Spannung und die wahre Dehnung kleiner als die technische Dehnung. Daher wird ein Punkt, der die wahre Spannungs-Dehnungs-Kurve definiert, nach oben und nach links verschoben, um die äquivalente technische Spannungs-Dehnungs-Kurve zu definieren. Die Differenz zwischen den wahren und den technischen Spannungen und Dehnungen nimmt mit der plastischen Verformung zu. Bei geringen Dehnungen (z. B. bei elastischer Verformung) sind die Unterschiede zwischen den beiden vernachlässigbar. Der Punkt der Zugfestigkeit ist der Maximalpunkt der technischen Spannungs-Dehnungs-Kurve, aber kein besonderer Punkt der echten Spannungs-Dehnungs-Kurve. Da die technische Spannung proportional zur Kraft ist, die entlang der Probe ausgeübt wird, kann das Kriterium für die Bildung von Einschnürungen wie folgt festgelegt werden $\delta F=0$. ⓘ

$\delta F=\sigma _{\text{t}}\,\delta A+A\,\delta \sigma _{\text{t}}=0$ ⓘ

$-{\tfrac {\delta A}{A}}={\tfrac {\delta \sigma _{\text{t}}}{\sigma _{\text{t}}}}$ ⓘ

Diese Analyse legt die Natur des UTS-Punktes nahe. Der Effekt der Arbeitsverfestigung wird durch das Schrumpfen der Querschnittsfläche am UTS-Punkt genau ausgeglichen. ⓘ

Nach der Bildung der Einschnürung erfährt die Probe eine heterogene Verformung, so dass die obigen Gleichungen nicht gültig sind. Die Spannung und Dehnung an der Einschnürung können wie folgt ausgedrückt werden:

$\sigma _{\text{t}}={\tfrac {F}{A_{\text{neck}}}}$

$\varepsilon _{\text{t}}=\ln \left({\tfrac {A_{0}}{A_{\text{neck}}}}\right)$ ⓘ

Zur Beschreibung des Verhältnisses zwischen echter Spannung und echter Dehnung wird in der Regel eine empirische Gleichung verwendet. ⓘ

$\sigma _{\text{t}}=K(\varepsilon _{\text{t}})^{n}$ ⓘ

Dabei ist $n$ der Kaltverfestigungskoeffizient und $K$ der Festigkeitskoeffizient ist. $n$ ist ein Maß für das Kalthärteverhalten eines Werkstoffs. Werkstoffe mit einem höheren $n$ haben einen größeren Widerstand gegen Einschnürungen. Typischerweise haben Metalle bei Raumtemperatur $n$ einen Wert zwischen 0,02 und 0,5. ⓘ

Stadien

Ein schematisches Diagramm der Spannungs-Dehnungs-Kurve von Stahl mit niedrigem Kohlenstoffgehalt bei Raumtemperatur ist in Abbildung 1 dargestellt. Es gibt mehrere Stufen, die unterschiedliche Verhaltensweisen zeigen, was auf unterschiedliche mechanische Eigenschaften schließen lässt. Zur Verdeutlichung: Werkstoffe können eine oder mehrere der in Abbildung 1 gezeigten Stufen nicht aufweisen, oder sie können völlig unterschiedliche Stufen haben. ⓘ

Die erste Stufe ist der linear elastische Bereich. Die Spannung ist proportional zur Dehnung, d. h. sie folgt dem allgemeinen Hooke'schen Gesetz, und die Steigung ist der Young'sche Modul. In diesem Bereich unterliegt das Material nur einer elastischen Verformung. Das Ende der Stufe ist der Anfangspunkt der plastischen Verformung. Die Spannungskomponente dieses Punktes wird als Streckgrenze (oder obere Streckgrenze, kurz UYP) definiert. ⓘ

Die zweite Stufe ist der Bereich der Kaltverfestigung. Dieser Bereich beginnt, wenn die Spannung über die Streckgrenze hinausgeht, und erreicht ein Maximum am Punkt der Bruchfestigkeit, der maximalen Spannung, die ausgehalten werden kann und als Bruchfestigkeit (UTS) bezeichnet wird. In diesem Bereich nimmt die Spannung hauptsächlich mit der Dehnung des Materials zu, außer dass es bei einigen Materialien wie Stahl zu Beginn einen nahezu flachen Bereich gibt. Die Spannung in diesem flachen Bereich wird als untere Streckgrenze (LYP) bezeichnet und ergibt sich aus der Bildung und Ausbreitung von Lüders-Bändern. Explizit bildet die heterogene plastische Verformung Bänder an der oberen Fließgrenze, und diese Bänder breiten sich mit der Verformung entlang der Probe an der unteren Fließgrenze aus. Nachdem die Probe wieder gleichmäßig verformt wurde, resultiert die Zunahme der Spannung mit dem Fortschreiten der Dehnung aus der Arbeitsverfestigung, d. h. dichte Versetzungen, die durch die plastische Verformung induziert werden, behindern die weitere Bewegung der Versetzungen. Um diese Hindernisse zu überwinden, sollte eine höhere aufgelöste Scherspannung angewendet werden. Mit zunehmender Dehnung wird die Arbeitsverfestigung verstärkt, bis die Spannung die endgültige Zugfestigkeit erreicht. ⓘ

Die dritte Stufe ist die Einschnürungszone. Jenseits der Zugfestigkeit bildet sich eine Einschnürung, bei der die lokale Querschnittsfläche deutlich kleiner als der Durchschnitt wird. Die Einschnürungsverformung ist heterogen und verstärkt sich selbst, da sich die Spannung stärker auf einen kleinen Abschnitt konzentriert. Eine solche positive Rückkopplung führt zu einer schnellen Entwicklung der Einschnürung und zum Bruch. Es ist zu beachten, dass die Zugkraft zwar abnimmt, die Verfestigung der Arbeit jedoch weiter voranschreitet, d. h. die tatsächliche Spannung steigt weiter an, die technische Spannung nimmt jedoch ab, da die schrumpfende Querschnittsfläche nicht berücksichtigt wird. In diesem Bereich kommt es schließlich zum Bruch. Nach dem Bruch können die prozentuale Dehnung und die Verringerung der Querschnittsfläche berechnet werden. ⓘ

Klassifizierung

Spannungs-Dehnungs-Kurve für spröde Materialien im Vergleich zu duktilen Materialien. ⓘ

Es ist möglich, einige gemeinsame Merkmale zwischen den Spannungs-Dehnungs-Kurven verschiedener Werkstoffgruppen zu unterscheiden und die Werkstoffe auf dieser Grundlage in zwei große Kategorien einzuteilen, nämlich in duktile und spröde Werkstoffe. ⓘ

Duktile Werkstoffe

Duktile Werkstoffe, zu denen Baustahl und viele Legierungen anderer Metalle gehören, zeichnen sich durch ihre Fähigkeit aus, bei normalen Temperaturen nachzugeben. ⓘ

Stahl mit niedrigem Kohlenstoffgehalt weist im Allgemeinen eine sehr lineare Spannungs-Dehnungs-Beziehung bis zu einer genau definierten Streckgrenze auf (Abb. 1). Der lineare Teil der Kurve ist der elastische Bereich, und die Steigung ist der Elastizitätsmodul oder der Youngsche Modul. Viele duktile Materialien, darunter einige Metalle, Polymere und Keramiken, weisen eine Fließgrenze auf. Das plastische Fließen setzt an der oberen Fließgrenze ein und setzt sich an der unteren fort. An der unteren Fließgrenze ist die bleibende Verformung heterogen über die Probe verteilt. Das Verformungsband, das sich an der oberen Fließgrenze gebildet hat, breitet sich entlang der Messlänge an der unteren Fließgrenze aus. Das Band nimmt die gesamte Messlänge an der unteren Streckgrenze ein. Jenseits dieses Punktes setzt die Kaltverfestigung ein. Das Auftreten der Fließgrenze ist mit dem Pinning von Versetzungen im System verbunden. Beispielsweise interagiert der Mischkristall mit den Versetzungen und wirkt wie ein Stift, der die Versetzung an der Bewegung hindert. Daher ist die Spannung, die erforderlich ist, um die Bewegung auszulösen, groß. Solange die Versetzung der Verankerung entkommt, ist die für die Fortsetzung der Bewegung erforderliche Spannung geringer. ⓘ

Nach der Fließgrenze nimmt die Kurve in der Regel leicht ab, da die Versetzungen aus den Cottrell-Atmosphären entweichen. Bei fortgesetzter Verformung nimmt die Spannung aufgrund der Kaltverfestigung zu, bis sie die höchste Zugspannung erreicht. Bis zu diesem Punkt nimmt die Querschnittsfläche aufgrund von Poisson-Kontraktionen gleichmäßig ab. Dann kommt es zur Einschnürung und schließlich zum Bruch. ⓘ

Das Auftreten von Einschnürungen in duktilen Werkstoffen hängt mit der geometrischen Instabilität des Systems zusammen. Aufgrund der natürlichen Inhomogenität des Materials finden sich in der Regel einige Bereiche mit kleinen Einschlüssen oder Porosität im Inneren oder an der Oberfläche, in denen sich die Dehnung konzentriert, was zu einer lokal kleineren Fläche als in anderen Bereichen führt. Bei einer Dehnung, die geringer ist als die ultimative Zugdehnung, ist der Anstieg der Kaltverfestigungsrate in diesem Bereich größer als die Flächenverringerungsrate, so dass sich dieser Bereich schwerer weiter verformen lässt als andere, so dass die Instabilität beseitigt wird, d. h. die Werkstoffe haben die Fähigkeit, die Inhomogenität zu schwächen, bevor die ultimative Dehnung erreicht wird. Mit zunehmender Dehnung nimmt jedoch die Verfestigungsrate ab, so dass der Bereich mit der kleineren Fläche schwächer ist als die anderen Bereiche, so dass sich die Flächenverringerung in diesem Bereich konzentriert und die Einschnürung bis zum Bruch immer ausgeprägter wird. Nachdem sich die Einschnürung in den Werkstoffen gebildet hat, konzentriert sich die weitere plastische Verformung auf die Einschnürung, während sich der Rest des Werkstoffs aufgrund des Rückgangs der Zugkraft elastisch zusammenzieht. ⓘ

Die Spannungs-Dehnungskurve für ein duktiles Material kann mit der Ramberg-Osgood-Gleichung angenähert werden. Diese Gleichung ist einfach zu implementieren und erfordert nur die Streckgrenze, die Bruchfestigkeit, den Elastizitätsmodul und die prozentuale Dehnung des Materials. ⓘ

Spröde Werkstoffe

Spröde Werkstoffe, zu denen Gusseisen, Glas und Stein gehören, zeichnen sich dadurch aus, dass sie brechen, ohne dass sich die Dehnungsrate zuvor merklich verändert hat; manchmal brechen sie auch, bevor sie nachgeben. ⓘ

Spröde Werkstoffe wie Beton oder Kohlenstofffasern haben keine genau definierte Streckgrenze und werden nicht kaltverfestigt. Daher sind die Bruchfestigkeit und die Reißfestigkeit identisch. Typische spröde Werkstoffe wie Glas zeigen keine plastische Verformung, sondern versagen, während die Verformung elastisch ist. Eines der Merkmale eines spröden Versagens ist, dass die beiden gebrochenen Teile wieder zusammengefügt werden können, um die gleiche Form wie das ursprüngliche Bauteil zu erhalten, da es keine Einschnürung wie bei duktilen Materialien gibt. Eine typische Spannungs-Dehnungs-Kurve für ein sprödes Material ist linear. Bei einigen Materialien, wie z. B. Beton, ist die Zugfestigkeit im Vergleich zur Druckfestigkeit vernachlässigbar und wird bei vielen technischen Anwendungen mit Null angenommen. Die Zugfestigkeit von Glasfasern ist höher als die von Stahl, die von massivem Glas jedoch in der Regel nicht. Dies ist auf den Spannungsintensitätsfaktor zurückzuführen, der mit Defekten im Material verbunden ist. Mit zunehmender Größe der Probe nimmt auch die erwartete Größe des größten Fehlers zu. ⓘ