Caesar-Verschlüsselung
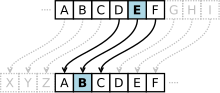
In der Kryptografie ist die Caesar-Chiffre, auch bekannt als Caesar-Chiffre, Shift-Chiffre, Caesar-Code oder Caesar-Shift, eine der einfachsten und bekanntesten Verschlüsselungstechniken. Es handelt sich um eine Art Substitutions-Chiffre, bei der jeder Buchstabe im Klartext durch einen Buchstaben an einer bestimmten Anzahl von Stellen im Alphabet ersetzt wird. Bei einer Linksverschiebung von 3 wird beispielsweise D durch A ersetzt, E wird zu B und so weiter. Die Methode ist nach Julius Cäsar benannt, der sie in seiner privaten Korrespondenz verwendete. ⓘ
Der Verschlüsselungsschritt einer Caesar-Chiffre wird häufig in komplexere Verfahren wie die Vigenère-Chiffre integriert und findet auch heute noch im ROT13-System Anwendung. Wie alle Substitutions-Chiffren mit nur einem Buchstaben ist auch die Caesar-Chiffre leicht zu knacken und bietet in der modernen Praxis im Wesentlichen keine Kommunikationssicherheit. ⓘ
Beispiel
Die Umwandlung kann durch Aneinanderreihung zweier Alphabete dargestellt werden; das Chiffrealphabet ist das reine Alphabet, das um eine bestimmte Anzahl von Positionen nach links oder rechts gedreht wurde. Hier ist zum Beispiel eine Caesar-Chiffre mit einer Linksdrehung um drei Stellen, was einer Rechtsverschiebung von 23 entspricht (der Verschiebungsparameter wird als Schlüssel verwendet):
| Einfaches | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z ⓘ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chiffre | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W |
Beim Verschlüsseln sucht eine Person jeden Buchstaben der Nachricht in der "Klartext"-Zeile und schreibt den entsprechenden Buchstaben in die "Chiffre"-Zeile. ⓘ
Klartext: DER SCHLAUE BRAUNE FUCHS SPRINGT ÜBER DEN FAULEN HUND
Chiffrierter Text: QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD ⓘ
Die Entschlüsselung erfolgt in umgekehrter Reihenfolge, mit einer Rechtsverschiebung von 3. ⓘ
Die Verschlüsselung kann auch durch modulare Arithmetik dargestellt werden, indem zunächst die Buchstaben in Zahlen umgewandelt werden, und zwar nach dem Schema A → 0, B → 1, ..., Z → 25. Die Verschlüsselung eines Buchstabens x durch eine Verschiebung n lässt sich mathematisch wie folgt beschreiben, ⓘ
Die Entschlüsselung erfolgt auf ähnliche Weise, ⓘ
(Es gibt verschiedene Definitionen für die Modulo-Operation. In der obigen Darstellung liegt das Ergebnis im Bereich von 0 bis 25, d. h. wenn x + n oder x - n nicht im Bereich von 0 bis 25 liegen, müssen wir 26 subtrahieren oder addieren). ⓘ
Die Ersetzung bleibt während der gesamten Nachricht gleich, so dass die Chiffre als eine Art monoalphabetische Substitution im Gegensatz zur polyalphabetischen Substitution eingestuft wird. ⓘ
Bei der Verschlüsselung wird jeder Buchstabe des Klartexts auf einen Geheimtextbuchstaben abgebildet. Diese Abbildung ergibt sich, indem man die Zeichen eines geordneten Alphabets um eine bestimmte Anzahl zyklisch nach rechts verschiebt (rotiert); zyklisch bedeutet, dass man beim Verschieben über Z hinaus wieder bei A anfangend weiterzählt. Die Anzahl der verschobenen Zeichen bildet den Schlüssel, der für die gesamte Verschlüsselung unverändert bleibt. Beispiel für eine Verschiebung um drei Zeichen:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z
Geheim: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C ⓘ
Aus dem Klartext „caesar“ wird somit der Geheimtext „FDHVDU“. Für die Entschlüsselung wird das Alphabet um dieselbe Anzahl Zeichen nach links rotiert. ⓘ
Geschichte und Verwendung

Die Caesar-Chiffre ist nach Julius Caesar benannt, der sie laut Suetonius mit einer Verschiebung von drei Buchstaben (A wird bei der Verschlüsselung zu D und D wird bei der Entschlüsselung zu A) verwendete, um Nachrichten von militärischer Bedeutung zu schützen. Obwohl Caesar dieses Schema zum ersten Mal verwendet hat, ist bekannt, dass andere Substitutions-Chiffren schon früher verwendet wurden.
"Wenn er etwas Vertrauliches zu sagen hatte, schrieb er es in Chiffre, das heißt, er änderte die Reihenfolge der Buchstaben des Alphabets so, dass kein einziges Wort zu erkennen war. Wenn jemand sie entziffern und ihren Sinn verstehen will, muss er den vierten Buchstaben des Alphabets, nämlich D, durch A ersetzen, und so auch die anderen."
- Suetonius, Leben des Julius Cäsar 56
Auch sein Neffe Augustus benutzte die Chiffre, allerdings mit einer Rechtsverschiebung um eins und ohne den Anfang des Alphabets zu umschreiben:
"Wann immer er in Chiffre schrieb, schrieb er B für A, C für B und den Rest der Buchstaben nach demselben Prinzip, wobei er AA für Z verwendete."
- Suetonius, Leben des Augustus 88
Es gibt Belege dafür, dass Julius Caesar auch kompliziertere Systeme verwendete, und ein Schriftsteller, Aulus Gellius, verweist auf eine (heute verlorene) Abhandlung über seine Chiffren:
"Es gibt sogar eine ziemlich raffiniert geschriebene Abhandlung des Grammatikers Probus über die geheime Bedeutung der Buchstaben bei der Abfassung von Caesars Briefen."
- Aulus Gellius, Attische Nächte 17.9.1-5 ⓘ
Es ist nicht bekannt, wie effektiv die Caesar-Chiffre zu dieser Zeit war, aber es ist wahrscheinlich, dass sie einigermaßen sicher war, nicht zuletzt, weil die meisten von Caesars Feinden Analphabeten waren und andere annahmen, dass die Nachrichten in einer unbekannten Fremdsprache geschrieben waren. Zu dieser Zeit gibt es keine Aufzeichnungen über Techniken zur Lösung einfacher Substitutions-Chiffren. Die frühesten erhaltenen Aufzeichnungen stammen aus den Werken von Al-Kindi aus dem 9. Jahrhundert in der arabischen Welt mit der Entdeckung der Frequenzanalyse. ⓘ
Eine Caesar-Chiffre mit einer Verschiebung von eins wird auf der Rückseite der Mezuzah verwendet, um die Namen Gottes zu verschlüsseln. Dies könnte ein Überbleibsel aus einer früheren Zeit sein, in der es Juden nicht erlaubt war, Mezuzot zu haben. Die Buchstaben des Kryptogramms selbst stellen einen religiös bedeutsamen "göttlichen Namen" dar, der nach orthodoxem Glauben die Kräfte des Bösen in Schach hält. ⓘ
Im 19. Jahrhundert wurde der Anzeigenteil von Zeitungen gelegentlich zum Austausch von Nachrichten genutzt, die mit einfachen Chiffrierverfahren verschlüsselt wurden. Kahn (1967) beschreibt Fälle, in denen Verliebte in der Times geheime Mitteilungen austauschten, die mit der Caesar-Chiffre verschlüsselt waren. Noch 1915 war die Caesar-Chiffre in Gebrauch: Die russische Armee setzte sie als Ersatz für kompliziertere Chiffren ein, deren Beherrschung sich für ihre Truppen als zu schwierig erwiesen hatte; deutsche und österreichische Kryptoanalytiker hatten wenig Schwierigkeiten, ihre Nachrichten zu entschlüsseln. ⓘ

Caesar-Chiffren finden sich heute in Kinderspielzeug wie geheimen Decoderringen. Eine Caesar-Verschiebung von dreizehn wird auch im ROT13-Algorithmus durchgeführt, einer einfachen Methode zur Verschleierung von Text, die im Usenet weit verbreitet ist und zur Verschleierung von Text (z. B. von Witzen und Spoilern) verwendet wird, aber nicht ernsthaft als Verschlüsselungsmethode eingesetzt wird. ⓘ
Die Vigenère-Chiffre verwendet eine Caesar-Chiffre mit einer anderen Verschiebung an jeder Position im Text; der Wert der Verschiebung wird durch ein sich wiederholendes Schlüsselwort definiert. Wenn das Schlüsselwort so lang ist wie die Nachricht, zufällig gewählt wird, nie jemand anderem bekannt wird und nie wiederverwendet wird, handelt es sich um die One-Time-Pad-Chiffre, die nachweislich unknackbar ist. Die Bedingungen sind so schwierig, dass sie in der Praxis nie erreicht werden. Schlüsselwörter, die kürzer als die Nachricht sind (z. B. "Complete Victory", das von der Konföderation während des amerikanischen Bürgerkriegs verwendet wurde), führen ein zyklisches Muster ein, das mit einer statistisch fortgeschrittenen Version der Frequenzanalyse entdeckt werden könnte. ⓘ
Im April 2006 wurde der flüchtige Mafiaboss Bernardo Provenzano in Sizilien gefasst, auch weil einige seiner Nachrichten, die er ungeschickt in einer Variante der Caesar-Chiffre geschrieben hatte, geknackt wurden. Provenzanos Chiffre verwendete Zahlen, so dass "A" als "4" geschrieben wurde, "B" als "5" und so weiter. ⓘ
Im Jahr 2011 wurde Rajib Karim im Vereinigten Königreich wegen "terroristischer Straftaten" verurteilt, nachdem er die Caesar-Chiffre zur Kommunikation mit islamischen Aktivisten aus Bangladesch verwendet hatte, um Pläne zur Sprengung von Flugzeugen der British Airways oder zur Störung ihrer IT-Netzwerke zu besprechen. Obwohl die Parteien Zugang zu weitaus besseren Verschlüsselungstechniken hatten (Karim selbst nutzte PGP für die Datenspeicherung auf Computerdisketten), entschieden sie sich für ihr eigenes (in Microsoft Excel implementiertes) System und lehnten ein ausgefeilteres Codeprogramm namens Mujahedeen Secrets ab, "weil die 'Kaffern', d. h. die Ungläubigen, davon wissen und es deshalb weniger sicher sein muss". Dies war eine Anwendung von Sicherheit durch Unklarheit. ⓘ
Sueton beschreibt das Verfahren wie folgt:
“[…] si qua occultius perferenda erant, per notas scripsit, id est sic structo litterarum ordine, ut nullum verbum effici posset: quae si quis investigare et persequi velit, quartam elementorum litteram, id est D pro A et perinde reliquas commutet.”
„[…] wenn etwas Geheimes zu überbringen war, schrieb er in Zeichen, das heißt, er ordnete die Buchstaben so, dass kein Wort gelesen werden konnte: Um diese zu lesen, tauscht man den vierten Buchstaben, also D für A aus und ebenso mit den restlichen.“ ⓘ
Leon Battista Alberti verbesserte das Verfahren im 15. Jahrhundert durch die Entwicklung der Chiffrierscheibe. Die Chiffrierscheibe erleichtert die Durchführung der Caesar-Verschlüsselung mit beliebigen Verschiebungen, indem die innere Scheibe um die Anzahl der verschobenen Buchstaben zur äußeren Scheibe gedreht wird und sich somit die ersetzten Buchstaben ablesen lassen. Darüber hinaus beschrieb Alberti auch die Verwendung der Chiffrierscheibe bzw. deren Varianten zur Durchführung von komplexeren monoalphabetischen und polyalphabetischen Substitutionsverfahren. ⓘ
1508 beschrieb Trithemius ein polyalphabetisches Substitutionsverfahren mit Hilfe der von ihm erfundenen Tabula recta. Dieses Verfahren, welches im 16. Jahrhundert als Vigenère-Verschlüsselung bekannt wurde, basiert im Wesentlichen auf der Caesar-Verschlüsselung, allerdings pro Buchstabe abwechselnd mit einer anderen Verschiebung, was die Sicherheit erheblich erhöht. ⓘ
Brechen der Chiffre
| Entschlüsselung Verschiebung |
Kandidat für den Klartext ⓘ |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
Die Caesar-Chiffre kann auch in einem Szenario, in dem nur der Chiffretext vorliegt, leicht gebrochen werden. Zwei Situationen können in Betracht gezogen werden:
- Ein Angreifer weiß (oder vermutet), dass eine einfache Substitutions-Chiffre verwendet wurde, aber nicht, dass es sich um ein Caesar-Schema handelt;
- ein Angreifer weiß, dass eine Caesar-Chiffre verwendet wird, kennt aber den Verschiebungswert nicht. ⓘ
Im ersten Fall kann die Chiffre mit denselben Techniken wie bei einer allgemeinen einfachen Substitutions-Chiffre geknackt werden, z. B. durch Frequenzanalyse oder Musterwörter. Beim Lösen der Chiffre wird ein Angreifer wahrscheinlich schnell die Regelmäßigkeit der Lösung bemerken und daraus schließen, dass es sich bei dem verwendeten Algorithmus um eine Caesar-Chiffre handelt. ⓘ

Im zweiten Fall ist es sogar noch einfacher, das Schema zu knacken. Da es nur eine begrenzte Anzahl möglicher Verschiebungen gibt (25 im Englischen), kann jede von ihnen nacheinander in einem Brute-Force-Angriff getestet werden. Eine Möglichkeit, dies zu tun, besteht darin, einen Ausschnitt des Chiffriertextes in eine Tabelle mit allen möglichen Verschiebungen zu schreiben - eine Technik, die manchmal als "Vervollständigung des Klartextes" bezeichnet wird. Das angegebene Beispiel bezieht sich auf den Chiffretext "EXXEGOEXSRGI"; der Klartext ist bei einer Verschiebung von vier sofort mit dem Auge erkennbar. Man kann sich diese Methode auch so vorstellen, dass unter jedem Buchstaben des Chiffretextes das gesamte Alphabet in umgekehrter Reihenfolge, beginnend mit diesem Buchstaben, ausgeschrieben wird. Dieser Angriff kann beschleunigt werden, indem man einen Satz von Streifen verwendet, auf denen das Alphabet in umgekehrter Reihenfolge aufgeschrieben ist. Die Streifen werden dann so ausgerichtet, dass der Chiffretext in einer Zeile steht, während der Klartext in einer der anderen Zeilen erscheinen sollte. ⓘ
Eine andere Methode besteht darin, die Häufigkeitsverteilung der Buchstaben abzugleichen. Wenn man die Häufigkeit der Buchstaben im Chiffretext grafisch darstellt und die erwartete Verteilung dieser Buchstaben in der Originalsprache des Klartextes kennt, kann ein Mensch den Wert der Verschiebung leicht erkennen, indem er die Verschiebung bestimmter Merkmale der Grafik betrachtet. Dies wird als Häufigkeitsanalyse bezeichnet. In der englischen Sprache sind zum Beispiel die Häufigkeiten der Buchstaben E, T (in der Regel am häufigsten) und Q, Z (in der Regel am seltensten) im Klartext besonders auffällig. Computer können dies auch tun, indem sie messen, wie gut die tatsächliche Häufigkeitsverteilung mit der erwarteten Verteilung übereinstimmt; zum Beispiel kann die Chi-Quadrat-Statistik verwendet werden. ⓘ
Bei Klartexten in natürlicher Sprache gibt es in der Regel nur eine plausible Entschlüsselung, obwohl bei extrem kurzen Klartexten mehrere Kandidaten möglich sind. Beispielsweise könnte der Chiffretext MPQY plausibel entweder zu "aden" oder "know" entschlüsselt werden (vorausgesetzt, der Klartext ist in englischer Sprache); ebenso "ALIIP" zu "dolls" oder "wheel"; und "AFCCP" zu "jolly" oder "cheer" (siehe auch Unizitätsdistanz). ⓘ
Bei der Caesar-Chiffre bietet die mehrfache Verschlüsselung eines Textes keine zusätzliche Sicherheit. Das liegt daran, dass zwei Verschlüsselungen, z. B. mit Shift A und Shift B, einer einzigen Verschlüsselung mit Shift A + B gleichkommen. ⓘ
Schlüsselbuchstabe
Die Verschiebung des Alphabets um N Zeichen (N = 1…25) stellt den Schlüssel dar. Statt die Verschiebung als Zahl anzugeben, kann man sie auch als Schlüsselbuchstaben angeben. Hierbei gibt es zwei gängige Konventionen:
- A entspricht keiner Verschiebung, B einer Verschiebung um 1, C einer Verschiebung um 2 usw.
- A entspricht einer Verschiebung um 1, B einer Verschiebung um 2, C einer Verschiebung um 3 usw. ⓘ
Die erste Konvention ergibt sich, wenn man den Schlüsselbuchstaben aus den beiden übereinander liegenden Alphabeten abliest („a“ auf „D“ ist eine Verschiebung um drei Zeichen). Dies ist auch bei der verwandten Vigenère-Verschlüsselung üblich. Zudem entspricht diese Konvention der Abbildung von Buchstabe auf Zahl, wie sie üblicherweise für die Modulo-Rechnung durchgeführt wird. Die zweite Konvention entspricht der natürlichen Nummerierung der Verschiebungen. Ein historischer Bezug, dass Caesar und Augustus jeweils ihren Anfangsbuchstaben als Schlüsselbuchstaben verwendeten, ist von Sueton nicht überliefert. ⓘ
Da sich beide Konventionen widersprechen, ist die Angabe eines Schlüsselbuchstabens missverständlich, die Angabe als Zahl hingegen eindeutig. ⓘ

