Wahrheitstabelle

Eine Wahrheitstabelle ist eine mathematische Tabelle, die in der Logik verwendet wird - insbesondere im Zusammenhang mit der booleschen Algebra, den booleschen Funktionen und der Aussagenkalkulation - und die die funktionalen Werte logischer Ausdrücke für jedes ihrer funktionalen Argumente, d. h. für jede Kombination von Werten, die die logischen Variablen annehmen, angibt. Insbesondere können Wahrheitstabellen verwendet werden, um zu zeigen, ob ein propositionaler Ausdruck für alle zulässigen Eingabewerte wahr, also logisch gültig ist. ⓘ

Eine Wahrheitstabelle hat eine Spalte für jede Eingabevariable (z. B. P und Q) und eine letzte Spalte, die alle möglichen Ergebnisse der logischen Operation zeigt, die die Tabelle darstellt (z. B. P XOR Q). Jede Zeile der Wahrheitstabelle enthält eine mögliche Konfiguration der Eingangsvariablen (z. B. P=wahr Q=falsch) und das Ergebnis der Operation für diese Werte. Zur weiteren Verdeutlichung siehe die Beispiele unten. Ludwig Wittgenstein wird im Allgemeinen die Erfindung und Popularisierung der Wahrheitstabelle in seinem Tractatus Logico-Philosophicus zugeschrieben, der 1918 fertiggestellt und 1921 veröffentlicht wurde. Ein solches System wurde 1921 auch unabhängig davon von Emil Leon Post vorgeschlagen. Eine noch frühere Version der Wahrheitstabelle wurde in unveröffentlichten Manuskripten von Charles Sanders Peirce aus dem Jahr 1893 gefunden, die beiden Veröffentlichungen um fast 30 Jahre vorausgingen. ⓘ

Animation zur Erstellung einer Wahrheitstafel ⓘ

Eine Wahrheitstabelle oder Wahrheitstafel, auch Wahrheitswert-Tabelle oder Wahrheitsmatrix genannt, ist eine tabellarische Aufstellung des Wahrheitswertverlaufs einer logischen Aussage. ⓘ

Die Wahrheitstabelle zeigt für alle möglichen Zuordnungen von endlich vielen (häufig zwei) Wahrheitswerten zu den aussagenlogisch nicht weiter zerlegbaren Teilaussagen, aus denen die Gesamtaussage zusammengesetzt ist, welchen Wahrheitswert die Gesamtaussage unter der jeweiligen Zuordnung annimmt. Die Wahrheitstabelle wird genutzt, um Wahrheitswertefunktionen beziehungsweise boolesche Funktionen darzustellen oder zu definieren und um einfache aussagenlogische Nachweise zu führen. Beispielsweise werden Wahrheitstabellen verwendet, um die Bedeutung von Junktoren festzulegen. ⓘ

Unäre Operationen

Es gibt 4 unäre Operationen:

Immer wahr
Nie wahr, unäres Falsum
Unäre Identität
Unäre Negation ⓘ

Logisch wahr

Der Ausgabewert ist immer wahr, unabhängig vom Eingabewert von p ⓘ

Logisch wahr ⓘ
p	$T$
T	T
F	T

Logisch falsch

Der Ausgabewert ist nie wahr, d. h. immer falsch, unabhängig vom Eingabewert von p ⓘ

Logisch falsch ⓘ
p	$F$
T	F
F	F

Logische Identität

Logische Identität ist eine Operation auf einem logischen Wert p, bei der der Ausgabewert p bleibt. ⓘ

Die Wahrheitstabelle für den logischen Identitätsoperator lautet wie folgt:

Logische Identität ⓘ
p	$p$
T	T
F	F

Logische Negation

Die logische Negation ist eine Operation auf einem logischen Wert, typischerweise dem Wert eines Satzes, die den Wert wahr ergibt, wenn ihr Operand falsch ist, und den Wert falsch, wenn ihr Operand wahr ist. ⓘ

Die Wahrheitstabelle für NOT p (auch als ¬p, Np, Fpq oder ~p geschrieben) lautet wie folgt:

Logische Negation ⓘ
p	$\negp$
T	F
F	T

Binäre Operationen

Es gibt 16 mögliche Wahrheitsfunktionen von zwei binären Variablen: ⓘ

Wahrheitstabelle für alle binären logischen Operatoren

Hier ist eine erweiterte Wahrheitstabelle mit Definitionen aller sechzehn möglichen Wahrheitsfunktionen von zwei booleschen Variablen P und Q:

p	q	F⁰	NOR¹	↚²	¬p³	↛⁴	¬q⁵	XOR⁶	NAND⁷	UND⁸	XNOR⁹	q¹⁰	→¹¹	p¹²	←¹³	ODER¹⁴	T^{15 ⓘ}
T	T	F	F	F	F	F	F	F	F	T	T	T	T	T	T	T	T
T	F	F	F	F	F	T	T	T	T	F	F	F	F	T	T	T	T
F	T	F	F	T	T	F	F	T	T	F	F	T	T	F	F	T	T
F	F	F	T	F	T	F	T	F	T	F	T	F	T	F	T	F	T
Com		✓	✓					✓	✓	✓	✓					✓	✓
Assoz.		✓						✓		✓	✓	✓		✓		✓	✓
Adj		F⁰	NOR¹	↛⁴	¬q⁵	↚²	¬p³	XOR⁶	NAND⁷	UND⁸	XNOR⁹	p¹²	←¹³	q¹⁰	→¹¹	ODER¹⁴	T¹⁵
Negativ		T¹⁵	ODER¹⁴	←¹³	p¹²	→¹¹	q¹⁰	XNOR⁹	UND⁸	NAND⁷	XOR⁶	¬q⁵	↛⁴	¬p³	↚²	NOR¹	F⁰
Dual		T¹⁵	NAND⁷	→¹¹	¬p³	←¹³	¬q⁵	XNOR⁹	NOR¹	ODER¹⁴	XOR⁶	q¹⁰	↚²	p¹²	↛⁴	UND⁸	F⁰
L id				F				F		T	T	T,F	T			F
R id						F		F		T	T			T,F	T	F

wobei ⓘ

T = wahr.

F = falsch.

Die hochgestellten Zahlen ⁰ bis ¹⁵ sind die Zahlen, die sich ergeben, wenn man die vier Wahrheitswerte als Binärzahl mit F = 0 und T = 1 liest.

Die Zeile Com gibt an, ob ein Operator, op, kommutativ ist - P op Q = Q op P.

Die Assoc-Zeile zeigt an, ob ein Operator, op, assoziativ ist - (P op Q) op R = P op (Q op R).

Die Adj-Zeile zeigt den Operator op2 an, so dass P op Q = Q op2 P

Die Neg-Reihe zeigt den Operator op2, so dass P op Q = ¬(P op2 Q)

Die Zeile Dual zeigt die duale Operation an, die sich aus der Vertauschung von T mit F und AND mit OR ergibt.

Die Zeile L id zeigt die linken Identitäten des Operators an, wenn er irgendwelche - Werte I hat, so dass I op Q = Q ist.

Die Zeile R id zeigt die rechten Identitäten des Operators an, wenn er beliebige - Werte I hat, so dass P op I = P ist. ⓘ

Die vier Kombinationen von Eingabewerten für p, q, werden zeilenweise aus der obigen Tabelle abgelesen. Die Ausgangsfunktion für jede Kombination von p, q kann zeilenweise aus der Tabelle abgelesen werden. ⓘ

Legende: Die folgende Tabelle ist nicht nach Zeilen, sondern nach Spalten geordnet. Es gibt vier Spalten und nicht vier Zeilen, um die vier Kombinationen von p, q als Eingabe anzuzeigen. ⓘ

p: T T F F
q: T F T F ⓘ

Dieser Schlüssel hat 16 Zeilen, eine Zeile für jede Binärfunktion der beiden Binärvariablen p, q. In Zeile 2 dieses Schlüssels ist zum Beispiel der Wert der umgekehrten Nichtimplikation (' $\nleftarrow$ ') ausschließlich T für die Spalte, die durch die eindeutige Kombination p=F, q=T bezeichnet wird; in Zeile 2 ist der Wert dieser ' $\nleftarrow$ ' für die drei verbleibenden Spalten p, q F ist. Die Ausgabezeile für $\nleftarrow$ ist also ⓘ

2: F F T F ⓘ

und der 16-zeilige Schlüssel lautet ⓘ

			Operator	Name der Operation ⓘ
0	(F F F F)(p, q)	⊥	falsch, Opq	Widersprüche
1	(F F F T)(p, q)	NOR	p ↓ q, Xpq	Logisches NOR
2	(F F T F)(p, q)	↚	p ↚ q, Mpq	Konverse Nichtimplikation
3	(F F T T)(p, q)	¬p, ~p	¬p, Np, Fpq	Negation
4	(F T F F)(p, q)	↛	p ↛ q, Lpq	Materielle Nichtimplikation
5	(F T F T)(p, q)	¬q, ~q	¬q, Nq, Gpq	Negation
6	(F T T F)(p, q)	XOR	p ⊕ q, Jpq	Exklusive Disjunktion
7	(F T T T)(p, q)	NAND	p ↑ q, Dpq	Logisches NAND
8	(T F F F)(p, q)	UND	p ∧ q, Kpq	Logische Konjunktion
9	(T F F T)(p, q)	XNOR	p Wenn und nur wenn q, Epq	Logische Zweibedingung
10	(T F T F)(p, q)	q	q, Hpq	Projektionsfunktion
11	(T F T T)(p, q)	p → q	wenn p dann q, Cpq	Materielle Implikation
12	(T T F F)(p, q)	p	p, Ipq	Projektionsfunktion
13	(T T F T)(p, q)	p ← q	p wenn q, Bpq	Umgekehrte Implikation
14	(T T T F)(p, q)	OR	p ∨ q, Apq	Logische Disjunktion
15	(T T T T)(p, q)	⊤	wahr, Vpq	Tautologie

Logische Operatoren können auch mit Hilfe von Venn-Diagrammen veranschaulicht werden. ⓘ

Logische Konjunktion (AND)

Die logische Konjunktion ist eine Operation auf zwei logischen Werten, typischerweise den Werten zweier Sätze, die den Wert wahr ergibt, wenn beide Operanden wahr sind. ⓘ

Die Wahrheitstabelle für p UND q (auch als p ∧ q, Kpq, p & q oder p $\cdot$ q) lautet wie folgt:

Logische Konjunktion ⓘ
p	q	p ∧ q
T	T	T
T	F	F
F	T	F
F	F	F

Wenn sowohl p als auch q wahr sind, dann ist die Konjunktion p ∧ q wahr. Für alle anderen Zuordnungen von logischen Werten zu p und zu q ist die Konjunktion p ∧ q falsch. ⓘ

Man kann auch sagen: Wenn p, dann ist p ∧ q gleich q, sonst ist p ∧ q gleich p. ⓘ

Logische Disjunktion (OR)

Die logische Disjunktion ist eine Operation für zwei logische Werte, in der Regel die Werte zweier Sätze, die den Wert wahr ergibt, wenn mindestens einer der Operanden wahr ist. ⓘ

Die Wahrheitstabelle für p ODER q (auch als p ∨ q, Apq, p || q oder p + q geschrieben) lautet wie folgt:

Logische Disjunktion ⓘ
p	q	p ∨ q
T	T	T
T	F	T
F	T	T
F	F	F

Auf Englisch ausgedrückt: Wenn p, dann ist p ∨ q p, andernfalls ist p ∨ q q. ⓘ

Logische Implikation

Die logische Implikation und das materielle Konditional sind beide mit einer Operation an zwei logischen Werten verbunden, in der Regel den Werten zweier Sätze, die einen Wert von falsch ergibt, wenn der erste Operand wahr und der zweite Operand falsch ist, und andernfalls einen Wert von wahr. ⓘ

Die Wahrheitstabelle für die logische Implikation p impliziert q (symbolisiert als p ⇒ q, oder seltener Cpq) lautet wie folgt:

Logische Implikation ⓘ
p	q	p ⇒ q
T	T	T
T	F	F
F	T	T
F	F	T

Die Wahrheitstabelle, die mit dem materiellen Konditional if p then q (symbolisiert als p → q) verbunden ist, lautet wie folgt:

Materielle Bedingung ⓘ
p	q	p → q
T	T	T
T	F	F
F	T	T
F	F	T

Es kann auch nützlich sein zu beachten, dass p ⇒ q und p → q äquivalent zu ¬p ∨ q sind. ⓘ

Logische Gleichheit

Logische Gleichheit (auch bekannt als bikonditional oder exclusive nor) ist eine Operation auf zwei logischen Werten, typischerweise den Werten zweier Sätze, die den Wert wahr ergibt, wenn beide Operanden falsch oder beide Operanden wahr sind. ⓘ

Die Wahrheitstabelle für p XNOR q (auch als p ↔ q, Epq, p = q oder p ≡ q geschrieben) lautet wie folgt:

Logische Gleichheit ⓘ
p	q	p ↔ q
T	T	T
T	F	F
F	T	F
F	F	T

p EQ q ist also wahr, wenn p und q denselben Wahrheitswert haben (beide wahr oder beide falsch), und falsch, wenn sie unterschiedliche Wahrheitswerte haben. ⓘ

Exklusive Disjunktion

Exklusive Disjunktion ist eine Operation mit zwei logischen Werten, typischerweise den Werten zweier Sätze, die den Wert wahr ergibt, wenn einer der Operanden wahr ist, aber nicht beide. ⓘ

Die Wahrheitstabelle für p XOR q (auch als Jpq oder p ⊕ q geschrieben) lautet wie folgt:

Exklusive Disjunktion ⓘ
p	q	p ⊕ q
T	T	F
T	F	T
F	T	T
F	F	F

Bei zwei Sätzen kann XOR auch als (p ∧ ¬q) ∨ (¬p ∧ q) geschrieben werden. ⓘ

Logisches NAND

Die logische NAND-Verknüpfung ist eine Operation mit zwei logischen Werten, typischerweise den Werten zweier Sätze, die den Wert falsch ergibt, wenn beide Operanden wahr sind. Mit anderen Worten: Sie ergibt den Wert wahr, wenn mindestens einer der Operanden falsch ist. ⓘ

Die Wahrheitstabelle für p NAND q (auch als p ↑ q, Dpq oder p | q geschrieben) lautet wie folgt:

Logisches NAND ⓘ
p	q	p ↑ q
T	T	F
T	F	T
F	T	T
F	F	T

Häufig ist es sinnvoll, eine logische Operation als zusammengesetzte Operation auszudrücken, d. h. als eine Operation, die aus anderen Operationen aufgebaut oder zusammengesetzt ist. Es sind viele solcher Zusammensetzungen möglich, je nachdem, welche Operationen als Grundoperationen oder "primitiv" und welche als zusammengesetzte oder "abgeleitete" Operationen betrachtet werden. ⓘ

Im Fall der logischen NAND-Verknüpfung ist sie eindeutig als eine Verbindung von NOT und AND darstellbar. ⓘ

Die Negation einer Konjunktion: ¬(p ∧ q), und die Disjunktion von Negationen: (¬p) ∨ (¬q) lassen sich wie folgt aufstellen:

p	q	p ∧ q	¬(p ∧ q)	¬p	¬q	(¬p) ∨ (¬q) ⓘ
T	T	T	F	F	F	F
T	F	F	T	F	T	T
F	T	F	T	T	F	T
F	F	F	T	T	T	T

Logisches NOR

Das logische NOR ist eine Operation auf zwei logischen Werten, typischerweise den Werten zweier Sätze, die den Wert wahr ergibt, wenn beide Operanden falsch sind. Mit anderen Worten, sie ergibt den Wert falsch, wenn mindestens einer ihrer Operanden wahr ist. ↓ ist auch als Peirce-Pfeil bekannt, nach seinem Erfinder Charles Sanders Peirce, und ist ein Sole-Addukt-Operator. ⓘ

Die Wahrheitstabelle für p NOR q (auch als p ↓ q oder Xpq geschrieben) lautet wie folgt:

Logisches NOR ⓘ
p	q	p ↓ q
T	T	F
T	F	F
F	T	F
F	F	T

Die Negation einer Disjunktion ¬(p ∨ q) und die Konjunktion der Negationen (¬p) ∧ (¬q) lassen sich wie folgt tabellieren:

p	q	p ∨ q	¬(p ∨ q)	¬p	¬q	(¬p) ∧ (¬q) ⓘ
T	T	T	F	F	F	F
T	F	T	F	F	T	F
F	T	T	F	T	F	F
F	F	F	T	T	T	T

Betrachtet man die tabellarischen Ableitungen für NAND und NOR unter jeder Zuordnung von logischen Werten zu den funktionalen Argumenten p und q, so ergeben sich für ¬(p ∧ q) die gleichen Muster von funktionalen Werten wie für (¬p) ∨ (¬q) und für ¬(p ∨ q) wie für (¬p) ∧ (¬q). Somit sind der erste und der zweite Ausdruck jedes Paares logisch äquivalent und können in allen Kontexten, die sich ausschließlich auf ihre logischen Werte beziehen, durch den jeweils anderen ersetzt werden. ⓘ

Diese Äquivalenz ist eines der Gesetze von De Morgan. ⓘ

Größe von Wahrheitstabellen

Wenn es n Eingangsvariablen gibt, dann gibt es 2n mögliche Kombinationen ihrer Wahrheitswerte. Eine gegebene Funktion kann für jede Kombination wahr oder falsch ergeben, so dass die Anzahl der verschiedenen Funktionen von n Variablen der doppelten Exponentialzahl 2²ⁿ entspricht. ⓘ

n	2ⁿ	2^{2^{n ⓘ}}
0	1	2
1	2	4
2	4	16
3	8	256
4	16	65,536
5	32	4,294,967,296	≈ 4.3×10⁹
6	64	18,446,744,073,709,551,616	≈ 1.8×10¹⁹
7	128	340,282,366,920,938,463,463,374,607,431,768,211,456	≈ 3.4×10³⁸
8	256	115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,936	≈ 1.2×10⁷⁷

Wahrheitstabellen für Funktionen mit drei oder mehr Variablen werden selten angegeben. ⓘ

Anwendungen

Wahrheitstabellen können verwendet werden, um viele andere logische Äquivalenzen zu beweisen. Betrachten wir zum Beispiel die folgende Wahrheitstabelle:

Logische Äquivalenz : $(p\Rightarrow q)\equiv (\lnot p\lor q)$ ⓘ
$p$	$q$	$\lnot p$	$\lnot p\lor q$	$p\Rightarrow q$
T	T	F	T	T
T	F	F	F	F
F	T	T	T	T
F	F	T	T	T

Dies zeigt die Tatsache, dass $p\Rightarrow q$ logisch äquivalent ist zu $\lnot p\lor q$ . ⓘ

Darstellung boolescher Funktionen

Für den zweiwertigen Fall wird der Wahrheitswert „wahr“ im Folgenden als $w$ und „falsch“ als $f$ bezeichnet. ⓘ

Für mehrwertige Fälle werden oft numerische Werte im Bereich von $0$ bis $1$ verwendet (im dreiwertigen Fall z. B. die Werte $0$ , ${\tfrac {1}{2}}=0{,}5$ und $1$ , im fünfwertigen Fall die Werte $0$ , ${\tfrac {1}{4}}=0{,}25$ , ${\tfrac {1}{2}}=0{,}5$ , ${\tfrac {3}{4}}=0{,}75$ und $1$ ). Im mehrwertigen Fall wird oft nicht von Wahrheitswerten, sondern von Quasiwahrheitswerten oder von Pseudowahrheitswerten gesprochen. ⓘ

Allgemein gibt es für eine m-wertige Logik, d. h. für eine Logik mit endlich vielen Wahrheitswerten, deren Anzahl m ist, $m^{m^{n}}$ n-stellige wahrheitsfunktionale Junktoren bzw. boolesche Funktionen. Für die zweiwertige Aussagenlogik gibt es also $2^{2^{1}}=4$ einstellige Junktoren und $2^{2^{2}}=16$ zweistellige Junktoren. Schon für die dreiwertige Aussagenlogik gibt es $3^{3^{1}}=27$ einstellige und $3^{3^{2}}=19\,683$ zweistellige Junktoren. ⓘ

Negation
$a$	$\lnot a$
w	f
f	w

Als ein Beispiel für eine einstellige Wahrheitswertefunktion einer zweiwertigen Logik dient hier die nebenstehende Wahrheitstafel, die das Ergebnis der Anwendung der Negation auf die Aussage

a

in der klassischen Aussagenlogik zeigt. ⓘ

Die folgende Tabelle gibt für jeden Wahrheitswert der Aussagen $a$ und $b$ das Resultat einiger zweiwertiger Verknüpfungen an:

Belegung		Konjunktion	Disjunktion	materiale Implikation	Äquivalenz Bikonditional ⓘ
$a$	$b$	AND	OR	Konditional	XNOR
w	w	w	w	w	w
w	f	f	w	f	f
f	w	f	w	w	f
f	f	f	f	w	w

Eine besondere Stellung haben folgende nach Henry Maurice Sheffer bzw. Charles Sanders Peirce benannte zweiwertige Funktionen (siehe hierzu Funktionale Vollständigkeit und Shefferscher Strich), denen das NAND- und das NOR-Gatter entsprechen:

$a$	$b$	Shefferscher Strich (NAND, $\|$ )	Peirce-Pfeil (NOR, $\downarrow$ ) ⓘ
w	w	f	f
w	f	w	f
f	w	w	f
f	f	w	w

In einer dreiwertigen Logik sind 19 683 zweistellige Verknüpfungen möglich. In der folgenden Tabelle sind zwei von ihnen dargestellt: Die Konjunktion aus der logischen Sprache Ł3 von Jan Łukasiewicz (1920) und die Konjunktion aus dem Kalkül B3 von Dmitrij Anatol'evič Bočvar (1938). ⓘ

Belegung		Konjunktion ⓘ
$a$	$b$	in Ł3	in B3
1	1	1	1
1	½	½	½
1	0	0	0
½	1	½	½
½	½	½	½
½	0	0	½
0	1	0	0
0	½	0	½
0	0	0	0

Eine vierwertige Logik hat bis zu $4^{4^{2}}=4\,294\,967\,296$ mögliche zweistelligen Operatoren. Hier als Beispiel die Wahrheitstafel für das Konditional bzw. die materiale Implikation im logischen System G4 von Kurt Gödel (1932). ⓘ

Belegung		Konditional ⓘ
$a$	$b$	in G4
1	1	1
1	²⁄₃	²⁄₃
1	¹⁄₃	¹⁄₃
1	0	0
²⁄₃	1	1
²⁄₃	²⁄₃	1
²⁄₃	¹⁄₃	¹⁄₃
²⁄₃	0	0
¹⁄₃	1	1
¹⁄₃	²⁄₃	1
¹⁄₃	¹⁄₃	1
¹⁄₃	0	0
0	1	1
0	²⁄₃	1
0	¹⁄₃	1
0	0	1

Verkürzte Wahrheitstabellen für binäre Operatoren

Für binäre Operatoren wird auch eine komprimierte Form der Wahrheitstabelle verwendet, bei der die Zeilen- und Spaltenüberschriften die Operanden und die Tabellenzellen das Ergebnis angeben. In der booleschen Logik wird beispielsweise diese komprimierte Wahrheitstabellennotation verwendet:

∧	F	T
F	F	F
T	F	T

∨	F	T ⓘ
F	F	T
T	T	T

Diese Notation ist besonders nützlich, wenn die Operationen kommutativ sind, obwohl man zusätzlich angeben kann, dass die Zeilen der erste Operand und die Spalten der zweite Operand sind. Diese komprimierte Notation ist besonders nützlich bei der Diskussion von mehrwertigen Erweiterungen der Logik, da sie die kombinatorische Explosion der sonst erforderlichen Anzahl von Zeilen erheblich reduziert. Sie sorgt auch für eine schnell erkennbare charakteristische "Form" der Verteilung der Werte in der Tabelle, die dem Leser helfen kann, die Regeln schneller zu erfassen. ⓘ

Wahrheitstabellen in der digitalen Logik

Wahrheitstabellen werden auch verwendet, um die Funktion von Hardware-Look-up-Tables (LUTs) in digitalen Logikschaltungen zu spezifizieren. Für eine LUT mit n Eingängen hat die Wahrheitstabelle 2^n Werte (oder Zeilen im obigen Tabellenformat), die eine boolesche Funktion für die LUT vollständig spezifizieren. Indem jeder boolesche Wert als Bit in einer Binärzahl dargestellt wird, können die Werte der Wahrheitstabelle in der EDA-Software (Electronic Design Automation) effizient als Ganzzahlwerte kodiert werden. So kann beispielsweise eine 32-Bit-Ganzzahl die Wahrheitstabelle für eine LUT mit bis zu 5 Eingängen kodieren. ⓘ

Bei Verwendung einer ganzzahligen Darstellung einer Wahrheitstabelle kann der Ausgabewert der LUT durch Berechnung eines Bitindex k auf der Grundlage der Eingabewerte der LUT ermittelt werden, wobei der Ausgabewert der LUT das k-te Bit der Ganzzahl ist. Um beispielsweise den Ausgabewert einer LUT bei einem Array von n booleschen Eingangswerten zu ermitteln, kann der Bitindex des Ausgabewerts der Wahrheitstabelle wie folgt berechnet werden: Wenn der i-te Eingang wahr ist, sei $V_{i}=1$ , sonst lass $V_{i}=0$ . Dann ist das k-te Bit der binären Darstellung der Wahrheitstabelle der Ausgangswert der LUT, wobei $k=V_{0}\times 2^{0}+V_{1}\times 2^{1}+V_{2}\times 2^{2}+\dots +V_{n}\times 2^{n}$ . ⓘ

Wahrheitstabellen sind eine einfache und unkomplizierte Möglichkeit, boolesche Funktionen zu kodieren. Da sie jedoch mit der Anzahl der Eingaben exponentiell anwachsen, sind sie für Funktionen mit einer großen Anzahl von Eingaben nicht geeignet. Andere Darstellungen, die mehr Speicherplatz benötigen, sind Textgleichungen und binäre Entscheidungsdiagramme. ⓘ

Anwendungen von Wahrheitstabellen in der digitalen Elektronik

In der digitalen Elektronik und der Informatik (Bereiche der angewandten Logik und Mathematik) können Wahrheitstabellen verwendet werden, um grundlegende boolesche Operationen auf einfache Korrelationen zwischen Eingängen und Ausgängen zu reduzieren, ohne dass logische Gatter oder Codes verwendet werden müssen. Zum Beispiel kann eine binäre Addition mit der Wahrheitstabelle dargestellt werden:

A B | C R
1 1 | 1 0
1 0 | 0 1
0 1 | 0 1
0 0 | 0 0 <span title="Aus: Englische Wikipedia, Abschnitt "Applications of truth tables in digital electronics"" class="plainlinks">[https://en.wikipedia.org/wiki/Truth_table#Applications_of_truth_tables_in_digital_electronics <span style="color:#dddddd">ⓘ</span>]</span>

wobei <span title="Aus: Englische Wikipedia, Abschnitt "Applications of truth tables in digital electronics"" class="plainlinks">[https://en.wikipedia.org/wiki/Truth_table#Applications_of_truth_tables_in_digital_electronics <span style="color:#dddddd">ⓘ</span>]</span>

A = Erster Operand
B = Zweiter Operand
C = Übertrag
R = Ergebnis

ⓘ

Diese Wahrheitstabelle wird von links nach rechts gelesen:

Das Wertepaar (A,B) ist gleich dem Wertepaar (C,R).
Oder für dieses Beispiel: A plus B gleich Ergebnis R, mit dem Übertrag C. ⓘ

Beachten Sie, dass diese Tabelle nicht die logischen Operationen beschreibt, die zur Durchführung dieser Operation erforderlich sind, sondern lediglich die Funktion der Eingänge zu den Ausgangswerten angibt. ⓘ

Was das Ergebnis betrifft, so kann dieses Beispiel arithmetisch als binäre Addition modulo 2 und logisch äquivalent zur binären Exklusiv-Oder-Operation (exklusive Disjunktion) betrachtet werden. ⓘ

In diesem Fall kann sie nur für sehr einfache Ein- und Ausgänge, wie 1 und 0, verwendet werden. Wenn jedoch die Anzahl der möglichen Werte an den Eingängen zunimmt, wird die Wahrheitstabelle größer. ⓘ

Bei einer Additionsoperation benötigt man beispielsweise zwei Operanden, A und B. Jeder von ihnen kann einen von zwei Werten haben, nämlich Null oder Eins. Die Anzahl der Kombinationen dieser beiden Werte ist 2×2, also vier. Das Ergebnis sind also vier mögliche Ausgänge von C und R. Würde man die Basis 3 verwenden, würde sich der Umfang auf 3×3, also neun mögliche Ausgänge erhöhen. ⓘ

Das erste "Additions"-Beispiel oben wird als Halbaddierer bezeichnet. Eine Volladdierung liegt vor, wenn der Übertrag aus der vorhergehenden Operation als Eingabe für den nächsten Addierer verwendet wird. Um die Logik eines Volladdierers zu beschreiben, wäre also eine Wahrheitstabelle mit acht Zeilen erforderlich:

A B C* | C R
0 0 0 | 0 0
0 1 0 | 0 1
1 0 0 | 0 1
1 1 0 | 1 0
0 0 1 | 0 1
0 1 1 | 1 0
1 0 1 | 1 0
1 1 1 | 1 1 <span title="Aus: Englische Wikipedia, Abschnitt "Applications of truth tables in digital electronics"" class="plainlinks">[https://en.wikipedia.org/wiki/Truth_table#Applications_of_truth_tables_in_digital_electronics <span style="color:#dddddd">ⓘ</span>]</span>

Wie vorher, aber...
C* = Übertrag vom vorherigen Addierer

ⓘ

Geschichte

Die Nachforschungen von Irving Anellis zeigen, dass C.S. Peirce der erste Logiker zu sein scheint (1893), der eine Wahrheitstabellenmatrix entwickelt hat. Aus der Zusammenfassung seiner Arbeit:

1997 entdeckte John Shosky auf der Rückseite einer Seite der maschinengeschriebenen Abschrift von Bertrand Russells Vorlesung von 1912 über "Die Philosophie des logischen Atomismus" Wahrheitstabellenmatrizen. Die Matrix für die Negation stammt von Russell, daneben befindet sich die Matrix für die materielle Implikation in der Hand von Ludwig Wittgenstein. Es wird gezeigt, dass ein unveröffentlichtes Manuskript, das als von Peirce 1893 verfasst identifiziert wurde, eine Wahrheitstabellenmatrix enthält, die der von John Shosky entdeckten Matrix für materielle Implikation gleichwertig ist. Ein unveröffentlichtes Manuskript von Peirce, das in den Jahren 1883-84 im Zusammenhang mit der Abfassung von Peirce' "On the Algebra of Logic: A Contribution to the Philosophy of Notation", das 1885 im American Journal of Mathematics erschien, enthält ein Beispiel für eine indirekte Wahrheitstabelle für das Konditional. ⓘ

Wenn man unter einer Wahrheitstabelle die homomorphe Zuordnung von Wahrheitswerten zu den in einer Aussage vorkommenden atomaren Aussagen versteht, dann geht die Wahrheitstabelle auf Philon von Megara zurück, der auf diese Weise im 4. Jahrhundert vor unserer Zeitrechnung die Wahrheitsfunktion für die materiale Implikation definierte. Auch in der von Chrysippos von Soloi geprägten stoischen Logik wurden Wahrheitstabellen in diesem Sinn umfassend verwendet. ⓘ

In der modernen Logik benutzte George Boole 1847 Wahrheitstafeln unter dem Namen „Module einer Funktion“ zur semantischen Entscheidbarkeit von logischen Termen (Funktionen). Später benützten auch Gottlob Frege und Charles Sanders Peirce dieses Entscheidungsverfahren, wobei Peirce den Zweck der Ermittlung von Tautologien deutlicher betonte. Wahrheitstabellen im wörtlichen Sinn als Tabellen wurden allerdings erst 1921 von Emil Leon Post und Ludwig Wittgenstein eingeführt; durch ihren Einfluss wurden Wahrheitstabellen als Verfahren zur Entscheidung für Tautologien Allgemeingut. ⓘ

Beweis- und Entscheidungsverfahren

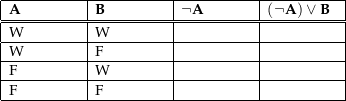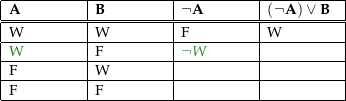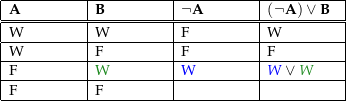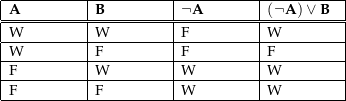
Wahrheitstabellen eignen sich dazu, einfache aussagenlogische Beweise auf der semantischen Modellebene zu führen, insbesondere für die Gültigkeit von grundlegenden Gesetzen, auf denen logische Beweisverfahren aufbauen. Zum Beispiel zeigt die logische Äquivalenz der 3. und 4. Spalte in den folgenden Wahrheitstabellen die Gültigkeit der De Morganschen Gesetze:

\lnot (a\land b)=(\lnot a)\lor (\lnot b)

$a$	$b$	$\lnot (a\land b)$	$(\lnot a)\lor (\lnot b)$
w	w	f	f
w	f	w	w
f	w	w	w
f	f	w	w

\lnot (a\lor b)=(\lnot a)\land (\lnot b)

ⓘ

$a$	$b$	$\lnot (a\lor b)$	$(\lnot a)\land (\lnot b)$
w	w	f	f
w	f	f	f
f	w	f	f
f	f	w	w

In der Praxis eignet sich diese Art der Beweisführung allerdings nur für Aussagen mit einer kleinen Anzahl von Aussagenvariablen, da die Größe exponentiell mit der Anzahl der Variablen wächst. ⓘ

Für die Aussagenlogik mit endlich vielen Wahrheitswerten und klassischem Folgerungsbegriff (siehe Klassische Logik) sind Wahrheitstafeln ein Entscheidungsverfahren für viele wichtige Fragestellungen, das heißt ein Verfahren, mit dem sich die jeweilige Fragestellung für jede Aussage in endlicher Zeit mechanisch entscheiden lässt. So lässt sich mit Hilfe von Wahrheitstafeln die Frage entscheiden, ob eine gegebene Aussage erfüllbar, unerfüllbar oder tautologisch ist (siehe Erfüllbarkeitsproblem der Aussagenlogik); ebenso lässt sich entscheiden, ob ein Argument gültig oder ungültig ist. ⓘ

Umformung in andere Darstellungsformen

Der Inhalt einer Wahrheitstabelle kann zur weiteren Verarbeitung oder Vereinfachung in andere, äquivalente Darstellungen überführt werden, beispielsweise in ein Karnaugh-Veitch-Diagramm. ⓘ

Eine Alternative: Wahrheitswertanalyse nach Quine

Wahrheitstabellen sind in vielen Fällen eine rationelle und einfach zu handhabende Methode der Wahrheitswertanalyse. Sie haben jedoch den Nachteil, dass immer alle Fälle durchgegangen werden müssen. Die Anzahl der Fälle steigt aber mit der Anzahl der Variablen (Satzbuchstaben) im Verhältnis $2^{n}$ an. Bei 2 Variablen gibt es 4 Fälle, bei 3 Variablen 8 Fälle, bei 4 Variablen 16 Fälle usw. Bei vielen Variablen kann die Wahrheitswertanalyse durch Wahrheitstabellen recht aufwändig werden. ⓘ

Deshalb schlägt Quine in seinem Buch Grundzüge der Logik eine alternative Form der Wahrheitswertanalyse vor. Auf Seite 54 gibt Quine das folgende Beispiel mit drei Variablen bzw. Satzbuchstaben (P, Q und R):

ⓘ

(P ∧ Q) ∨ (¬P ∧ ¬R) → (Q ↔ R)

(w ∧ Q) ∨ (f ∧ ¬R) → (Q ↔ R)

(f ∧ Q) ∨ (w ∧ ¬R) → (Q ↔ R)

Q ∨ (f ∧ ¬R) → (Q ↔ R)

f ∨ (w ∧ ¬R) → (Q ↔ R)

(Q ∨ f) → (Q ↔ R)

(w ∧ ¬R) → (Q ↔ R)

Q → (Q ↔ R)

¬R → (Q ↔ R)

w → (w ↔ R)

f → (f ↔ R)

f → (Q ↔ w)

w → (Q ↔ f)

w ↔ R

w

Q ↔ f

R

¬Q

w

f

w

Der Beispielterm (P ∧ Q) ∨ (¬P ∧ ¬R) → (Q ↔ R) ist also in zwei Fällen falsch: bei P/w|Q/w|R/f und bei P/f|Q/w|R/f. Die Wahrheitstabelle dazu sieht so aus:

P	Q	R	(P	∧	Q)	∨	(¬P	∧	¬R)	→	(Q	↔	R) ⓘ
w	w	w	w	w	w	w	f	f	f	w	w	w	w
w	w	f	w	w	w	w	f	f	w	f	w	f	f
w	f	w	w	f	f	f	f	f	f	w	f	f	w
w	f	f	w	f	f	f	f	f	w	w	f	w	f
f	w	w	f	f	w	f	w	f	f	w	w	w	w
f	w	f	f	f	w	w	w	w	w	f	w	f	f
f	f	w	f	f	f	f	w	f	f	w	f	f	w
f	f	f	f	f	f	w	w	w	w	w	f	w	f

Ein einfacheres Beispiel ist die Definition der Implikation: (A → B) ↔ (¬A ∨ B) ⓘ

Die Wahrheitstabelle dazu sieht so aus:

A	B	(A	→	B)	↔	(¬A	∨	B) ⓘ
w	w	w	w	w	w	f	w	w
w	f	w	f	f	w	f	f	f
f	w	f	w	w	w	w	w	w
f	f	f	w	f	w	w	w	f

Die Wahrheitswertanalyse nach Quine sieht bei diesem Beispiel so aus:

ⓘ

(A → B) ↔ (¬A ∨ B)

(w → B) ↔ (f ∨ B)

(f → B) ↔ (w ∨ B)

(w → w) ↔ (f ∨ w)

(w → f) ↔ (f ∨ f)

(w ↔ w)

(w → w)

(f ↔ f)

w

Bei der von Quine vorgeschlagenen Methode der Wahrheitswertanalyse werden die Variablen bzw. Satzbuchstaben also schrittweise durch ihre Wahrheitswerte ersetzt. Dabei werden dann zeilenweise Fallunterscheidungen vorgenommen, so dass eine baumartige Struktur entsteht. In beiden Beispielen, dem von Quine und der Definition der Implikation, ist auch zu sehen, dass nicht immer alle Fälle durchgegangen werden müssen, was bei vielen Variablen ein Vorteil gegenüber Wahrheitstabellen sein kann. Durch beide Methoden können die Fälle, in denen ein Term wahr bzw. falsch wird exakt ermittelt werden. Daher leisten beide Methoden dasselbe, sind also äquivalent. ⓘ

P	Q	R	(P	∧	Q)	∨	(¬P	∧	¬R)	→	(Q	↔	R) ⓘ
w	w	w	w	w	w	w	f	f	f	w	w	w	w
w	w	f	w	w	w	w	f	f	w	f	w	f	f
w	f	w	w	f	f	f	f	f	f	w	f	f	w
w	f	f	w	f	f	f	f	f	w	w	f	w	f
f	w	w	f	f	w	f	w	f	f	w	w	w	w
f	w	f	f	f	w	w	w	w	w	f	w	f	f
f	f	w	f	f	f	f	w	f	f	w	f	f	w
f	f	f	f	f	f	w	w	w	w	w	f	w	f

P	Q	R	(P	∧	Q)	∨	(¬P	∧	¬R)	→	(Q	↔	R) ⓘ
w	w	w	w	w	w	w	f	f	f	w	w	w	w
w	w	f	w	w	w	w	f	f	w	f	w	f	f
w	f	w	w	f	f	f	f	f	f	w	f	f	w
w	f	f	w	f	f	f	f	f	w	w	f	w	f
f	w	w	f	f	w	f	w	f	f	w	w	w	w
f	w	f	f	f	w	w	w	w	w	f	w	f	f
f	f	w	f	f	f	f	w	f	f	w	f	f	w
f	f	f	f	f	f	w	w	w	w	w	f	w	f

P	Q	R	(P	∧	Q)	∨	(¬P	∧	¬R)	→	(Q	↔	R) ⓘ
w	w	w	w	w	w	w	f	f	f	w	w	w	w
w	w	f	w	w	w	w	f	f	w	f	w	f	f
w	f	w	w	f	f	f	f	f	f	w	f	f	w
w	f	f	w	f	f	f	f	f	w	w	f	w	f
f	w	w	f	f	w	f	w	f	f	w	w	w	w
f	w	f	f	f	w	w	w	w	w	f	w	f	f
f	f	w	f	f	f	f	w	f	f	w	f	f	w
f	f	f	f	f	f	w	w	w	w	w	f	w	f