Prozessfähigkeitsindex
Bei der Prozessverbesserung ist der Prozessfähigkeitsindex oder das Prozessfähigkeitsverhältnis ein statistisches Maß für die Prozessfähigkeit: die Fähigkeit eines Prozesses, einen Output innerhalb der Spezifikationsgrenzen zu produzieren. Das Konzept der Prozessfähigkeit ist nur für Prozesse von Bedeutung, die sich in einem Zustand der statistischen Kontrolle befinden. Prozessfähigkeitsindizes messen, wie viel "natürliche Variation" ein Prozess im Verhältnis zu seinen Spezifikationsgrenzen erfährt, und ermöglichen es, verschiedene Prozesse im Hinblick darauf zu vergleichen, wie gut eine Organisation sie kontrolliert. ⓘ
Die Prozessfähigkeitsindizes Cp und CpK sind Kennzahlen zur statistischen Bewertung eines Prozesses in der Produktionstechnik. Sie geben an, wie sicher die laut Spezifikation vorgegebenen Ziele erreicht werden. ⓘ
Beispiel für Nicht-Fachleute
Ein Unternehmen stellt auf einer Drehbank Achsen mit einem Nenndurchmesser von 20 mm her. Da keine Achse exakt auf 20 mm gefertigt werden kann, gibt der Konstrukteur die maximal zulässigen Abweichungen (Toleranzen oder Spezifikationsgrenzen genannt) an. Die Vorgabe könnte zum Beispiel lauten, dass die Achsen zwischen 19,9 und 20,2 mm groß sein müssen. Der Prozessfähigkeitsindex ist ein Maß dafür, wie wahrscheinlich es ist, dass eine produzierte Achse diese Anforderung erfüllt. Der Index bezieht sich nur auf statistische (natürliche) Abweichungen. Dabei handelt es sich um Abweichungen, die natürlicherweise und ohne spezifische Ursache auftreten. Zu den nicht berücksichtigten Fehlern gehören Bedienerfehler oder ein Spiel in den Mechanismen der Drehmaschine, das zu einer falschen oder unvorhersehbaren Werkzeugposition führt. Treten solche Fehler auf, ist der Prozess nicht statistisch beherrscht. Ist dies der Fall, ist der Prozessfähigkeitsindex bedeutungslos. ⓘ
Einführung
Wenn die obere und die untere Spezifikationsgrenze des Prozesses USL und LSL sind, ist der Zielmittelwert des Prozesses T, der geschätzte Mittelwert des Prozesses ist und die geschätzte Variabilität des Prozesses (ausgedrückt als Standardabweichung) ist dann sind die allgemein anerkannten Prozessfähigkeitsindizes folgende:
| Index | Beschreibung ⓘ |
|---|---|
| Schätzt, was der Prozess zu produzieren vermag, wenn der Prozessmittelwert zwischen den Spezifikationsgrenzen zentriert wäre. Geht davon aus, dass der Prozessoutput annähernd normalverteilt ist. | |
| Schätzt die Prozessfähigkeit für Spezifikationen, die nur aus einer Untergrenze bestehen (z. B. Festigkeit). Es wird angenommen, dass der Prozessoutput annähernd normalverteilt ist. | |
| Schätzt die Prozessfähigkeit für Spezifikationen, die nur aus einem oberen Grenzwert bestehen (z. B. Konzentration). Es wird angenommen, dass der Prozessoutput annähernd normalverteilt ist. | |
| Schätzt ab, was der Prozess produzieren kann, wobei berücksichtigt wird, dass der Prozessmittelwert möglicherweise nicht zwischen den Spezifikationsgrenzen zentriert ist. (Wenn der Prozessmittelwert nicht zentriert ist, wird die Prozessfähigkeit überschätzt.) wenn der Prozessmittelwert außerhalb der Spezifikationsgrenzen liegt. Geht davon aus, dass der Prozessoutput annähernd normalverteilt ist. | |
| Schätzt die Prozessfähigkeit um einen Zielwert, T. ist immer größer als Null. Geht davon aus, dass der Prozessoutput annähernd normalverteilt ist. ist auch als Taguchi-Fähigkeitsindex bekannt. | |
| Schätzt die Prozessfähigkeit um einen Zielwert, T, und berücksichtigt einen außermittigen Prozessmittelwert. Setzt voraus, dass der Prozessoutput annähernd normalverteilt ist. |
wird anhand der Standardabweichung der Stichprobe geschätzt. ⓘ
Empfohlene Werte
Prozessfähigkeitsindizes sind so konstruiert, dass sie mit zunehmend höheren Werten eine wünschenswerte Fähigkeit ausdrücken. Werte nahe oder unter Null weisen auf Prozesse hin, die außerhalb des Ziels ( weit von T) oder mit hoher Streuung arbeiten. ⓘ
Die Festlegung von Werten für minimale "akzeptable" Prozessfähigkeitsziele ist eine Frage der persönlichen Meinung, und der Konsens, der besteht, variiert je nach Branche, Anlage und dem betrachteten Prozess. In der Automobilindustrie beispielsweise legt die Automotive Industry Action Group im Production Part Approval Process, 4. Auflage, Richtlinien für empfohlene Cpk-Mindestwerte für qualitätskritische Prozessmerkmale fest. Diese Kriterien sind jedoch umstritten, und mehrere Prozesse werden möglicherweise nicht auf ihre Fähigkeit hin bewertet, nur weil sie nicht richtig beurteilt wurden. ⓘ
Da die Prozessfähigkeit eine Funktion der Spezifikation ist, ist der Prozessfähigkeitsindex nur so gut wie die Spezifikation. Wenn die Spezifikation beispielsweise aus einer technischen Richtlinie stammt, ohne die Funktion und Kritikalität des Teils zu berücksichtigen, ist eine Diskussion über die Prozessfähigkeit nutzlos und würde mehr Nutzen bringen, wenn man sich auf die tatsächlichen Risiken eines Teils außerhalb der Spezifikation konzentrieren würde. Die Verlustfunktion von Taguchi veranschaulicht dieses Konzept besser. ⓘ
Mindestens ein akademischer Experte empfiehlt das Folgende:
| Situation | Empfohlene Mindestprozessfähigkeit für zweiseitige Spezifikationen | Empfohlene Mindestprozessfähigkeit bei einseitiger Spezifikation ⓘ |
|---|---|---|
| Bestehender Prozess | 1.33 | 1.25 |
| Neues Verfahren | 1.50 | 1.45 |
| Sicherheitsrelevante oder kritische Parameter für den bestehenden Prozess | 1.50 | 1.45 |
| Sicherheits- oder kritische Parameter für den neuen Prozess | 1.67 | 1.60 |
| Six Sigma Qualitätsprozess | 2.00 | 2.00 |
Wenn jedoch ein Prozess ein Merkmal mit einem Fähigkeitsindex von mehr als 2,5 erzeugt, kann die unnötige Präzision teuer werden. ⓘ
Beziehung zu Maßen des Prozessabfalls
Die Zuordnung von Prozessfähigkeitsindizes, wie z. B. Cpk, zu Maßen für den Prozessausfall ist einfach. Der Prozessausfall gibt an, wie viele Fehler ein Prozess produziert und wird durch DPMO oder PPM gemessen. Die Prozessausbeute ist das Komplement des Prozessausfalles und entspricht ungefähr der Fläche unter der Wahrscheinlichkeitsdichtefunktion wenn der Prozessoutput annähernd normalverteilt ist. ⓘ
Auf kurze Sicht ("kurzes Sigma") sind die Beziehungen wie folgt:
| Cp | Sigma-Niveau (σ) | Fläche unter der
Wahrscheinlichkeitsdichtefunktion |
Prozessausbeute | Prozess-Fallout
(in Form von DPMO/PPM) ⓘ |
|---|---|---|---|---|
| 0.33 | 1 | 0.6826894921 | 68.27% | 317311 |
| 0.67 | 2 | 0.9544997361 | 95.45% | 45500 |
| 1.00 | 3 | 0.9973002039 | 99.73% | 2700 |
| 1.33 | 4 | 0.9999366575 | 99.99% | 63 |
| 1.67 | 5 | 0.9999994267 | 99.9999% | 1 |
| 2.00 | 6 | 0.9999999980 | 99.9999998% | 0.002 |
Langfristig können sich die Prozesse erheblich verschieben oder driften (die meisten Regelkarten reagieren nur auf Veränderungen von 1,5σ oder mehr im Prozessoutput). Bei einer 1,5-Sigma-Verschiebung der Prozesse um 1,5σ gegenüber dem Ziel (siehe Six Sigma) würden sich diese Beziehungen ergeben:
| Cp | Angepasst
Sigma-Niveau (σ) |
Fläche unter der
Wahrscheinlichkeitsdichtefunktion |
Prozessausbeute | Prozess-Fallout
(in Form von DPMO/PPM) ⓘ |
|---|---|---|---|---|
| 0.33 | 1 | 0.3085375387 | 30.85% | 691462 |
| 0.67 | 2 | 0.6914624613 | 69.15% | 308538 |
| 1.00 | 3 | 0.9331927987 | 93.32% | 66807 |
| 1.33 | 4 | 0.9937903347 | 99.38% | 6209 |
| 1.67 | 5 | 0.9997673709 | 99.9767% | 232.6 |
| 2.00 | 6 | 0.9999966023 | 99.99966% | 3.40 |
Da sich Prozesse langfristig erheblich verschieben oder driften können, hätte jeder Prozess einen eigenen Sigma-Verschiebungswert, so dass Prozessfähigkeitsindizes weniger geeignet sind, da sie eine statistische Kontrolle erfordern. ⓘ
Beispiel
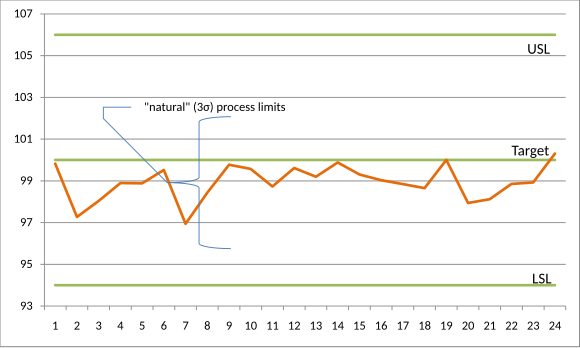
Nehmen wir ein Qualitätsmerkmal mit einem Zielwert von 100,00 μm und oberen und unteren Spezifikationsgrenzen von 106,00 μm bzw. 94,00 μm. Wenn nach sorgfältiger Überwachung des Prozesses über einen gewissen Zeitraum hinweg der Eindruck entsteht, dass der Prozess beherrscht wird und vorhersehbare Ergebnisse liefert (wie im nachstehenden Ablaufdiagramm dargestellt), können wir den Mittelwert und die Standardabweichung sinnvoll schätzen. ⓘ
Wenn und auf 98,94 μm bzw. 1,03 μm geschätzt werden, dann ⓘ
| Index ⓘ |
|---|
Die Tatsache, dass der Prozess exzentrisch läuft (etwa 1σ unter dem Zielwert), spiegelt sich in den deutlich unterschiedlichen Werten für Cp, Cpk, Cpm und Cpkm wider. ⓘ
Definition
Folgende Formeln gelten nur für normalverteilte Merkmale. In der DIN ISO 22514-2 (ehem. DIN ISO 21747) finden sich Berechnungsmethoden, die anwendbar für alle Verteilungsmodelle sind. ⓘ
Der CpK-Wert wird folgendermaßen aus dem Mittelwert , der dazugehörigen Standardabweichung und der oberen () beziehungsweise unteren () Spezifikationsgrenze definiert:
Je höher dieser Wert ist, desto sicherer befindet sich die gesamte Produktion innerhalb der Spezifikation. ⓘ
Der Cp-Wert ist definiert als:
Der Cp-Wert lässt sich nur dann berechnen, wenn sowohl eine obere als auch untere Spezifikationsgrenze definiert ist. ⓘ
Während der Cp-Wert nur das Verhältnis der vorgegebenen Toleranz zur Prozessstreuung angibt, beinhaltet der CpK-Wert auch die Lage des Mittelwertes zur vorgegebenen Toleranzmitte. Im besten Fall (Prozessmittelwert liegt genau in der Mitte des Toleranzbereichs) ist CpK = Cp; sonst ist CpK < Cp. ⓘ
Die einzelnen Buchstaben der Abkürzung stehen für:
- C: Capability
- p: process
- K: Katayori (japanisch), was soviel heißt wie „Bias“ oder „Verschiebung“. ⓘ
Zielwerte
Früher wurde ein CpK-Wert von mindestens 1,00 (der Abstand der nächstgelegenen Toleranzgrenze vom Prozessmittelwert beträgt mindestens 3 Standardabweichungen) als ausreichend angesehen, später wurde die Forderung auf 1,33 (4 Standardabweichungen) angehoben. Mittlerweile wird vielfach ein Cp-Wert von 2,00 (die Breite des Toleranzbereichs entspricht einer Streubreite von ±6 Standardabweichungen, daher Six Sigma) kombiniert mit einem CpK-Wert von 1,67 (der Abstand der nächstgelegenen Toleranzgrenze vom Prozessmittelwert beträgt mindestens 5 Standardabweichungen) als wünschenswertes Ziel definiert. Zu beachten ist, dass naturgemäß ein Gesamtsystem aus vielen Komponenten eine wesentlich höhere Fehlerrate hat als die Einzelkomponenten. Für einen genügend hohen CpK-Wert des Systems müssen die Komponenten einen noch deutlich höheren Wert aufweisen. ⓘ
Vergleichstabelle CpK - PPM
Unter der Annahme einer normalverteilten Prozessgröße lässt sich aus dem Prozessfähigkeitsindex CpK über die folgende Formel die Anzahl der zu erwartenden Fehler je 1 Million (parts per million) berechnen: ⓘ
Dabei ist die Verteilungsfunktion der Standardnormalverteilung. Die folgende Tabelle gibt einige Beispielwerte für die zweiseitige Wahrscheinlichkeit:
| CpK | PPM | Sigma ⓘ |
|---|---|---|
| 0,50 | 133614 | |
| 0,67 | 45500 | |
| 0,79 | 20000 | |
| 0,90 | 6933 | |
| 1,00 | 2699 | 3σ |
| 1,30 | 96 | |
| 1,33 | 66 | 4σ |
| 1,42 | 20 | |
| 1,50 | 3,4 | |
| 1,60 | 2 | |
| 1,67 | 0,6 | 5σ |
| 2,00 | 0,002 | 6σ |
Wenn die Annahme einer Normalverteilung nicht erfüllt ist, dann ist der Zusammenhang zwischen Index und Fehlerrate in PPM ein anderer. Oft sind Daten z. B. log-normal oder Student-T verteilt. In diesen beiden Fällen ist der PPM-Wert für einen Index von beispielsweise 1.5 weitaus kleiner als bei einer Normalverteilung, umgekehrt wäre es bei einer Rechteckverteilung (Gleichverteilung). Aus diesem Grund sollte man einen Normalitätstest ausführen. Dieser kann aber bei zu kleiner Datenmenge ungenau sein. ⓘ
Kritik
Der Cp- und Cpk-Wert haben eine Aussage, wenn eine Normalverteilung vorliegt. Das einfachste Mittel, um die Prozessfähigkeit eines gegebenen Prozesses zu steigern, besteht darin, die Spezifikationsgrenzen zu lockern: Je größer die Differenz zwischen OSG und USG, desto mehr Standardabweichungen lassen sich darin unterbringen. Durch den Wegfall von Spezifikationsgrenzen wird eine unendliche Prozessfähigkeit erreicht. ⓘ
Damit die Prozessfähigkeit ein sinnvolles Maß bleibt, dürfen die Spezifikationsgrenzen in keinem Fall vom Prozesseigner beeinflussbar sein. ⓘ
Je höher der geforderte Cpk-Wert, desto weniger können die zum Beispiel in der Zeichnung vorgegebenen Merkmalstoleranzen ausgenutzt werden. ⓘ





![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{USL}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{LSL}} \over 3{\hat {\sigma }}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca677d2001052bf0545a61bde6b3fd5d269dedb8)








![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{USL}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{LSL}} \over 3{\hat {\sigma }}}{\Bigg ]}=\min {\Bigg [}{106.00-98.94 \over 3\times 1.03},{98.94-94 \over 3\times 1.03}{\Bigg ]}=1.60}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a1d39f30f9d41b5b0943cb55654b788b191324)









