Trachtenberg-System

Das Trachtenberg-System ist ein System des schnellen Kopfrechnens. Das System besteht aus einer Reihe von leicht auswendig zu lernenden Operationen, die es ermöglichen, arithmetische Berechnungen sehr schnell durchzuführen. Es wurde von dem russischen Ingenieur Jakow Trachtenberg entwickelt, um sich während seiner Zeit im Konzentrationslager der Nazis zu beschäftigen. ⓘ

Im weiteren Verlauf dieses Artikels werden einige von Trachtenberg entwickelte Methoden vorgestellt. Einige der von Trachtenberg entwickelten Algorithmen sind solche für die allgemeine Multiplikation, Division und Addition. Außerdem enthält das Trachtenberg-System einige spezielle Methoden für die Multiplikation kleiner Zahlen zwischen 5 und 13 (hier jedoch 2-12). ⓘ

Der Abschnitt über die Addition zeigt eine effektive Methode zur Überprüfung von Berechnungen, die auch auf die Multiplikation angewendet werden kann ⓘ

Allgemeine Multiplikation, Trachtenberg-Matheorie

Die Methode der allgemeinen Multiplikation ist eine Methode, um Multiplikationen $a\times b$ mit geringer Platzkomplexität, d. h. mit möglichst wenigen Zwischenergebnissen, die im Speicher gehalten werden müssen. Dies wird dadurch erreicht, dass die Endziffer vollständig durch die Multiplikation der letzten Ziffer der Multiplikanden bestimmt wird. Diese wird als Zwischenergebnis festgehalten. Um die vorletzte Stelle zu finden, brauchen wir alles, was diese Stelle beeinflusst: Das vorläufige Ergebnis, die letzte Ziffer von $a$ mal der vorletzten Stelle von $b$, sowie die vorletzte Ziffer von $a$ mal der letzten Ziffer von $b$. Diese Berechnung wird durchgeführt, und wir erhalten ein vorläufiges Ergebnis, das in den letzten beiden Ziffern korrekt ist. ⓘ

Im Allgemeinen wird für jede Stelle $n$ im Endergebnis die Summe für alle $i$:

$a{\text{ (digit at }}i{\text{ )}}\times b{\text{ (digit at }}(n-i){\text{)}}.$ ⓘ

Man kann diesen Algorithmus erlernen und so vierstellige Zahlen im Kopf multiplizieren, indem man nur das Endergebnis aufschreibt. Sie würden mit der äußersten rechten Ziffer beginnen und mit der äußersten linken Ziffer aufhören. ⓘ

Trachtenberg definierte diesen Algorithmus mit einer Art paarweiser Multiplikation, bei der zwei Ziffern mit einer Ziffer multipliziert werden, wobei im Wesentlichen nur die mittlere Ziffer des Ergebnisses erhalten bleibt. Wenn man den obigen Algorithmus mit dieser paarweisen Multiplikation durchführt, müssen noch weniger Zwischenergebnisse gespeichert werden. ⓘ

Beispiel: $123456\times 789$ ⓘ

Um die erste (ganz rechte) Ziffer der Antwort zu finden, beginnen Sie mit der ersten Ziffer des Multiplikanden:

Die Einerstelle von $9\times 6\ is\ 4.$

Die erste Ziffer der Antwort ist $4$. Die zehnte Stelle $5$ wird ignoriert. ⓘ

Zeiger für die erste Ziffer ⓘ

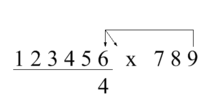
Um die zweite Ziffer der Antwort zu ermitteln, beginnt man mit der zweiten Ziffer des Multiplikanden:

Die Einerstelle von $9\times 5$ plus die Zehnerstelle von $9\times 6$ plus

Die Einerstelle von $8\times 6$.

$5+5+8=18$.

Die zweite Ziffer der Antwort ist $8$ und übertrage $1$ zur dritten Ziffer. ⓘ

Zeiger für die zweite Ziffer ⓘ

Um die dritte Ziffer der Antwort zu finden, beginnt man bei der dritten Ziffer des Multiplikanden:

Die Einerstelle von $9\times 4$ plus die Zehnerstelle von $9\times 5$ plus

Die Einerstelle von $8\times 5$ plus die Zehnerstelle von $8\times 6$ plus

Die Einerstelle von $7\times 6$

$1+6+4+0+4+2=17$

Die dritte Stelle der Antwort ist $7$ und übertrage $1$ bis zur nächsten Ziffer. ⓘ

Zeiger für die dritte Ziffer ⓘ

Um die vierte Ziffer der Antwort zu finden, beginnt man bei der vierten Ziffer des Multiplikanden:

Die Einerstelle von $9\times 3$ plus die Zehnerstelle von $9\times 4$ plus

Die Einerstelle von $8\times 4$ plus die Zehnerstelle von $8\times 5$ plus

Die Einerstelle von $7\times 5$ plus die Zehnerstelle von $7\times 6$.

$1+7+3+2+4+5+4=26$ Übertragen von der dritten Ziffer.

Die vierte Ziffer der Antwort lautet $6$ und übertrage $2$ bis zur nächsten Ziffer. ⓘ

Fahren Sie mit der gleichen Methode fort, um die restlichen Ziffern zu erhalten. ⓘ

2-Finger-Methode

Trachtenberg nannte dies die 2-Finger-Methode. Die Berechnungen zur Ermittlung der vierten Ziffer aus dem obigen Beispiel sind rechts dargestellt. Der Pfeil von der Neun zeigt immer auf die Stelle des Multiplikanden, die direkt über der Stelle der gesuchten Antwort liegt, wobei die anderen Pfeile jeweils eine Stelle nach rechts zeigen. Jede Pfeilspitze zeigt auf ein UT-Paar oder ein Produkt-Paar. Der senkrechte Pfeil zeigt auf das Produkt, bei dem wir die Einerstelle erhalten, und der schräge Pfeil zeigt auf das Produkt, bei dem wir die Zehnerstellen des Produktpaares erhalten. Wenn ein Pfeil auf ein Feld ohne Ziffer zeigt, wird für diesen Pfeil keine Berechnung durchgeführt. Beim Lösen der einzelnen Ziffern verschieben Sie die Pfeile über dem Multiplikanden jeweils um eine Ziffer nach links, bis alle Pfeile auf vorangestellte Nullen zeigen. ⓘ

Vorbereitung auf die Division ⓘ

Die Division im Trachtenberg-System erfolgt in ähnlicher Weise wie die Multiplikation, jedoch mit Subtraktion statt Addition. Durch Aufteilung des Dividenden in kleinere Teildividenden und anschließende Division dieser Teildividende durch die äußerste linke Ziffer des Divisors erhält man die Antwort Ziffer für Ziffer. Beim Lösen jeder Ziffer der Antwort subtrahiert man dann Produktpaare (UT-Paare) und auch NT-Paare (Zahl-Zehner) von der Teildividende, um die nächste Teildividende zu finden. Die Produktpaare werden zwischen den Ziffern der bisherigen Antwort und dem Divisor gefunden. Wenn eine Subtraktion eine negative Zahl ergibt, muss man eine Ziffer zurückgehen und diese Ziffer der Antwort um eins verringern. Mit genügend Übung kann man diese Methode im Kopf durchführen. ⓘ

Zwei-Finger Methode ⓘ

Allgemeine Addition

Eine Methode, um Zahlenkolonnen zu addieren und das Ergebnis genau zu überprüfen, ohne die erste Operation zu wiederholen. Es wird eine Zwischensumme in Form von zwei Ziffernreihen gebildet. Die Antwort erhält man, indem man die Summe der Zwischenergebnisse mit einem L-förmigen Algorithmus bildet. Als letzter Schritt wird eine Prüfmethode empfohlen, die zum einen das Risiko der Wiederholung von ursprünglichen Fehlern ausschließt und zum anderen die Spalte, in der ein Fehler auftritt, auf einmal identifiziert. Sie basiert auf Prüfsummen (oder Ziffernsummen), wie z. B. der Neuner-Rest-Methode. ⓘ

Damit das Verfahren wirksam ist, müssen die verschiedenen Operationen, die in den einzelnen Phasen verwendet werden, voneinander getrennt werden, da sonst die Gefahr von Interferenzen besteht. ⓘ

Andere Multiplikationsalgorithmen

Bei der Durchführung eines dieser Multiplikationsalgorithmen sollten die folgenden "Schritte" beachtet werden. ⓘ

Die Antwort muss ziffernweise ermittelt werden, wobei mit der niedrigstwertigen Ziffer begonnen und nach links gegangen wird. Die letzte Berechnung bezieht sich auf die führende Null des Multiplikanden. ⓘ

Jede Ziffer hat einen Nachbarn, d. h. die Ziffer zu ihrer Rechten. Der Nachbar der rechten Ziffer ist die hintere Null. ⓘ

Die Operation "Halbieren" hat im Trachtenberg-System eine besondere Bedeutung. Sie soll "die Hälfte der Ziffer, abgerundet" bedeuten, aber aus Geschwindigkeitsgründen werden die Anhänger des Trachtenberg-Systems dazu angehalten, diese Halbierung sofort vorzunehmen. Anstatt also zu denken: "Die Hälfte von sieben ist dreieinhalb, also drei", wird vorgeschlagen, dass man "sieben, drei" denkt. Das beschleunigt das Rechnen erheblich. Auf dieselbe Weise sollen die Tabellen für die Subtraktion von Ziffern von 10 oder 9 auswendig gelernt werden. ⓘ

Und immer dann, wenn die Regel verlangt, die Hälfte des Nachbarn zu addieren, sollte man immer 5 addieren, wenn die aktuelle Ziffer ungerade ist. Damit wird der Wegfall von 0,5 bei der Berechnung der nächsten Ziffer kompensiert. ⓘ

Multiplizieren mit 2

Beweis ⓘ

$R=T*2\Leftrightarrow R=2*(10^{n-1}*c_{n}+\ldots +10^{0}*c_{1})\Leftrightarrow R=10^{n-1}*2*c_{n}+\ldots +10^{0}*2*c_{1}$ ⓘ

Die Regel: Multipliziere jede Ziffer mit 2 (mit Übertrag). ⓘ

Beispiel: 8624 × 2 ⓘ

Von links nach rechts arbeiten:

8+8=16,

6+6=12 (Übertrag der 1),

2+2=4

4+4=8;

8624 × 2 = 17248 ⓘ

Beispiel: 76892 × 2 ⓘ

Von links nach rechts arbeiten:

7+7=14

6+6=12

8+8=16

9+9=18

2+2=4;

76892 × 2 =153784 ⓘ

Multiplizieren mit 3

Beweis ⓘ

${\begin{aligned}R&=T*3\\&=3*(10^{n-1}*c_{n}+\ldots +10^{0}*c_{1})\\&=(10/2-2)*(10^{n-1}*c_{n}+10^{n-2}*c_{n-1}+\ldots +10^{0}*c_{1})\\&=10^{n}*(c_{n}/2-2)+10^{n}*2+10^{n-1}*(c_{n-1}/2-2)+10^{n-1}*2+\ldots +10^{1}*(c_{1}/2-2)+10^{1}*2\\&\quad -2*(10^{n-1}*c_{n}+10^{n-2}*c_{n-1}+\ldots +10^{1}*c_{2}+10^{0}*c_{1})\\&=10^{n}*(c_{n}/2-2)+10^{n-1}*(c_{n-1}/2+20-2-2*c_{n})+10^{n-2}*(c_{n-2}/2+20-2-2*c_{n-1})\\&\quad +\ldots +10^{1}*(c_{1}/2+20-2-2*c_{2})+10^{0}*(20-2*c_{1})\\&=10^{n}*(c_{n}/2-2)+10^{n-1}*(2*(9-c_{n})+c_{n-1}/2)+10^{n-2}*(2*(9-c_{n-1})+c_{n-2}/2)\\&\quad +\ldots +10^{1}*(2*(9-c_{2})+c_{1}/2)+10^{0}*(2*(10-c_{1}))\\\end{aligned}}$ ⓘ

dotsvert setR gegen setN: a = (a ital "div" b)*b + (a mod b) ⓘ

R = 10^n*(((c_n ital "div" 2)*2 + (c_n mod 2))/2 - 2) + 10^(n-1)*(2*(9 - c_n) + c_{n-1}/2) + 10^(n-2)*(2*(9 - c_{n-1}) + c_{n-2}/2) ⓘ

" " + ... + 10^1*(2*(9 - c_2) + c_1/2) + 10^0*(2*(10 - c_1)) \Leftrightarrow ⓘ

R = 10^n*((c_n ital "div" 2) - 2) + 10^(n-1)*(10*(c_n mod 2)/2 + 2*(9 - c_n) + c_{n-1}/2) + 10^(n-2)*(2*(9 - c_{n-1}) + c_{n-2}/2) " " + ... + 10^1*(2*(9 - c_2) + c_1/2) + 10^0*(2*(10 - c_1)) \Leftrightarrow ⓘ

R = 10^n*((c_n ital "div" 2) - 2) + 10^(n-1)*(2*(9 - c_n) + c_{n-1}/2 + (c_n mod 2)*5) + 10^(n-2)*(2*(9 - c_{n-1}) + c_{n-2}/2) " " + ... + 10^1*(2*(9 - c_2) + c_1/2) + 10^0*(2*(10 - c_1)) \Leftrightarrow ⓘ

R = 10^n*((c_n ital "div" 2) - 2) + 10^(n-1)*(2*(9 - c_n) + (c_{n-1} ital "div" 2) + hvis(c_n mod 2 <> 0; 5;0)) " " + ... + 10^1*(2*(9 - c_2) + (c_1 ital "div" 2) + hvis(c_2 mod 2 <> 0; 5;0)) " " + 10^0*(2*(10 - c_1) + hvis(c_1 mod 2 <> 0; 5;0))</math> ⓘ

Regel:

1. Subtrahiere die äußerste rechte Ziffer von 10.
2. Subtrahiere die restlichen Ziffern von 9.
3. Verdopple das Ergebnis.
4. Addiere die Hälfte der rechten Nachbarziffer, plus 5, wenn die Ziffer ungerade ist.
5. Für die führende Null ziehst du 2 von der Hälfte der Nachbarziffer ab. ⓘ

Beispiel: 492 × 3 = 1476 ⓘ

Von rechts nach links arbeiten:

(10 - 2) × 2 + die Hälfte von 0 (0) = 16. Schreibe 6, übertrage 1.

(9 - 9) × 2 + die Hälfte von 2 (1) + 5 (da 9 ungerade ist) + 1 (Übertrag) = 7. Schreibe 7.

(9 - 4) × 2 + die Hälfte von 9 (4) = 14. Schreibe 4, übertrage 1.

Die Hälfte von 4 (2) - 2 + 1 (Übertrag) = 1. Schreibe 1. ⓘ

Multiplizieren mit 4

Regel:

1. Subtrahiere die äußerste rechte Ziffer von 10.
   1. Subtrahiere die restlichen Ziffern von 9.
2. Addiere die Hälfte der Nachbarziffer, plus 5, wenn die Ziffer ungerade ist.
3. Für die führende 0 subtrahiere 1 von der Hälfte der Nachbarziffer. ⓘ

Beispiel: 346 × 4 = 1384 ⓘ

Von rechts nach links arbeiten:

(10 - 6) + Hälfte von 0 (0) = 4. Schreibe 4.

(9 - 4) + Hälfte von 6 (3) = 8. Schreibe 8.

(9 - 3) + Hälfte von 4 (2) + 5 (da 3 ungerade ist) = 13. Schreibe 3, übertrage 1.

Die Hälfte von 3 (1) - 1 + 1 (Übertrag) = 1. Schreibe 1. ⓘ

Multiplikation mit 5

• Die Regel: Nimm die Hälfte des Nachbarn, dann, wenn die aktuelle Ziffer ungerade ist, addiere 5.

Beispiel: 42×5=210

Die Hälfte der Nachbarstelle von 2, die hintere Null, ist 0.

Die Hälfte der Nachbarstelle von 4 ist 1.

Die Hälfte der Nachbarstelle der führenden Null ist 2.

43×5 = 215

Die Hälfte des Nachbars von 3 ist 0, plus 5, weil 3 ungerade ist, ist 5.

Die Hälfte der Nachbarstelle von 4 ist 1.

Die Hälfte der Nachbarstelle der führenden Null ist 2.

93×5=465

Die Hälfte des Nachbars von 3 ist 0, plus 5, weil 3 ungerade ist, ist 5.

Die Hälfte von 9s Nachbar ist 1, plus 5, weil 9 ungerade ist, ist 6.

Die Hälfte des Nachbars der führenden Null ist 4. ⓘ

Multiplizieren mit 6

Regel:

1. Zu jeder Ziffer wird die Hälfte der Nachbarziffer addiert. Wenn die aktuelle Ziffer ungerade ist, addiere 5. ⓘ

Beispiel: 357 × 6 = 2142 ⓘ

Von rechts nach links arbeiten:

7 hat keinen Nachbarn, addiere 5 (da 7 ungerade ist) = 12. Schreibe 2, übertrage die 1.

5 + die Hälfte von 7 (3) + 5 (da die Anfangszahl 5 ungerade ist) + 1 (übertragen) = 14. Schreibe 4, übertrage die 1.

3 + die Hälfte von 5 (2) + 5 (da 3 ungerade ist) + 1 (übertragen) = 11. Schreibe 1, übertrage 1.

0 + die Hälfte von 3 (1) + 1 (Übertrag) = 2. Schreibe 2. ⓘ

Multiplikation mit 7

Regel:

1. Verdopple jede Ziffer.
2. Addiere die Hälfte der Nachbarziffer (ohne Nachkommastellen, falls vorhanden).
3. Wenn die Grundziffer ungerade ist, addiere 5. ⓘ

Beispiel: 523 × 7 = 3,661 ⓘ

Von rechts nach links arbeiten:

3×2 + 0 + 5 = 11, 1.

2×2 + 1 + 1 = 6.

5×2 + 1 + 5 = 16, 6.

0×2 + 2 + 1 = 3. ⓘ

Multiplizieren mit 8

Regel:

1. Subtrahiere die äußerste rechte Ziffer von 10.
   1. Subtrahiere die restlichen Ziffern von 9.
2. Verdopple das Ergebnis.
3. Addiere die Nachbarstelle.
4. Für die führende Null ziehst du 2 von der Nachbarstelle ab. ⓘ

Beispiel: 456 × 8 = 3648 ⓘ

Von rechts nach links arbeiten:

(10 - 6) × 2 + 0 = 8. Schreiben Sie 8. ⓘ

(9 - 5) × 2 + 6 = 14, Schreibe 4, übertrage 1. ⓘ

(9 - 4) × 2 + 5 + 1 (Übertrag) = 16. Schreibe 6, übertrage 1. ⓘ

4 - 2 + 1 (Übertrag) = 3. Schreibe 3. ⓘ

Multiplizieren mit 9

Regeln:

1. Subtrahiere die äußerste rechte Ziffer von 10.
   1. Subtrahiere die restlichen Ziffern von 9.
2. Addiere die Nachbarzahl zur Summe
3. Für die führende Null subtrahiere 1 von der Nachbarzahl. ⓘ

Bei den Regeln 9, 8, 4 und 3 wird nur die erste Ziffer von 10 subtrahiert. Danach wird jede Ziffer stattdessen von neun subtrahiert. ⓘ

Beispiel: 2,130 × 9 = 19,170 ⓘ

Von rechts nach links arbeiten:

(10 - 0) + 0 = 10. Schreibe 0, übertrage 1.

(9 - 3) + 0 + 1 (Übertrag) = 7. Schreibe 7.

(9 - 1) + 3 = 11. Schreibe 1, übertrage 1.

(9 - 2) + 1 + 1 (Übertrag) = 9. Schreibe 9.

2 - 1 = 1. Schreibe 1. ⓘ

Multiplizieren mit 11

Beweis ⓘ

${\begin{aligned}R&=T*11\\&=T*(10+1)\\&=10*T+T\\&=(10^{n}*c_{n}+\ldots +10^{1}*c_{1})+(10^{n-1}*c_{n}+\ldots +10^{0}*c_{1})\\&=10^{n}*c_{n}+10^{n-1}*(c_{n}+c_{n-1})+\ldots +10^{1}*(c_{2}+c_{1})+c_{1}\end{aligned}}$ ⓘ

Regel:

1. Addiere die Ziffer zu ihrer Nachbarin. (Mit "Nachbar" meinen wir die Ziffer auf der rechten Seite.) ⓘ

Beispiel: $3,425\times 11=37,675$

(0 + 3) (3 + 4) (4 + 2) (2 + 5) (5 + 0)

3 7 6 7 5 ⓘ

Zur Veranschaulichung:

11=10+1 ⓘ

So,

$3425\times 11=3425\times (10+1)$

$\rightarrow 37675=34250+3425$ ⓘ

Multiplizieren mit 12

Regel: Multiplizieren mit 12:
Beginnend mit der Ziffer ganz rechts, jede Ziffer verdoppeln und die Nachbarziffer addieren. (Der "Nachbar" ist die Ziffer auf der rechten Seite.) ⓘ

Ist das Ergebnis größer als eine einzelne Ziffer, wird die zusätzliche Ziffer (eine 1 oder 2) einfach auf die nächste Operation übertragen. Die verbleibende Ziffer ist eine Ziffer des Endergebnisses. ⓘ

Beispiel: $316\times 12$ ⓘ

Bestimmen Sie die Nachbarn des Multiplikanden 0316:

• Ziffer 6 hat keinen rechten Nachbarn
• Ziffer 1 hat den Nachbarn 6
• Ziffer 3 hat den Nachbarn 1
• Ziffer 0 (die vorangestellte Null) hat den Nachbarn 3

${\begin{aligned}6\times 2&=12{\text{ (2 carry 1) }}\\1\times 2+6+1&=9\\3\times 2+1&=7\\0\times 2+3&=3\\0\times 2+0&=0\\[10pt]316\times 12&=3,792\end{aligned}}$ ⓘ

Veröffentlichungen

• Rushan Ziatdinov, Sajid Musa. Schnelles mentales Rechensystem als Werkzeug für die Entwicklung des algorithmischen Denkens von Grundschülern. European Researcher 25(7): 1105-1110, 2012 [1].
• Das Trachtenberg Speed System of Basic Mathematics von Jakow Trachtenberg, A. Cutler (Übersetzer), R. McShane (Übersetzer), wurde von Doubleday and Company, Inc. Garden City, New York im Jahr 1960 veröffentlicht. ⓘ

Das Buch enthält spezifische algebraische Erklärungen für jede der oben genannten Operationen. ⓘ

Die meisten Informationen in diesem Artikel stammen aus dem Originalbuch. ⓘ

Die Algorithmen/Operationen für die Multiplikation usw. können auf andere, kompaktere Weise ausgedrückt werden, die im Buch trotz des Kapitels über die algebraische Beschreibung nicht angegeben sind. ⓘ

In der Populärkultur

Der amerikanische Film Gifted aus dem Jahr 2017 dreht sich um ein Wunderkind, das im Alter von 7 Jahren seine Lehrerin beeindruckt, indem es mit dem Trachtenberg-System im Kopf rechnet. ⓘ

Andere Systeme

Es gibt viele andere Rechenmethoden in der Kopfmathematik. In der folgenden Liste sind einige andere Rechenmethoden aufgeführt, auch wenn sie nicht unbedingt rein mental sind. ⓘ

• Bharati Krishna Tirtha's Buch "Vedische Mathematik"
• Mentaler Abakus - Wenn die Schüler sich daran gewöhnt haben, den Abakus mit den Fingern zu bedienen, werden sie in der Regel gebeten, den Abakus in ihrem Kopf zu visualisieren. Fast alle geübten Abakus-Benutzer sind auch im Kopfrechnen versiert.
• Chisanbop ⓘ

Allgemeine Division

Dividiert wird im Trachtenberg-System sehr ähnlich der Trachtenberg'schen Multiplikation, aber mit Subtraktion statt Addition. ⓘ