Lagrange-Multiplikator

In der mathematischen Optimierung ist die Methode der Lagrange-Multiplikatoren eine Strategie zum Auffinden der lokalen Maxima und Minima einer Funktion unter Gleichheitsbedingungen (d. h. unter der Bedingung, dass eine oder mehrere Gleichungen durch die gewählten Werte der Variablen genau erfüllt werden müssen). Benannt ist es nach dem Mathematiker Joseph-Louis Lagrange. Die Grundidee besteht darin, ein eingeschränktes Problem in eine Form umzuwandeln, bei der der Ableitungstest eines nicht eingeschränkten Problems weiterhin angewendet werden kann. Die Beziehung zwischen dem Gradienten der Funktion und den Gradienten der Nebenbedingungen führt ganz natürlich zu einer Neuformulierung des ursprünglichen Problems, die als Lagrangesche Funktion bezeichnet wird. ⓘ

Die Methode lässt sich wie folgt zusammenfassen: Um das Maximum oder Minimum einer Funktion zu finden $f(x)$ zu finden, die der Gleichheitsbeschränkung $g(x)=0$zu finden, bilden Sie die Lagrangesche Funktion

${\mathcal {L}}(x,\lambda )=f(x)+\lambda g(x)$

und finden Sie die stationären Punkte von ${\mathcal {L}}$ als eine Funktion von $x$ und dem Lagrange-Multiplikator $\lambda$Dies bedeutet, dass alle partiellen Ableitungen gleich Null sein sollten, einschließlich der partiellen Ableitung in Bezug auf $\lambda$. Die Lösung, die der ursprünglichen eingeschränkten Optimierung entspricht, ist immer ein Sattelpunkt der Lagrangeschen Funktion, der unter den stationären Punkten aufgrund der Definitheit der begrenzten hessischen Matrix identifiziert werden kann. ⓘ

Der große Vorteil dieser Methode besteht darin, dass sie es ermöglicht, die Optimierung ohne explizite Parametrisierung in Bezug auf die Nebenbedingungen zu lösen. Infolgedessen wird die Methode der Lagrange-Multiplikatoren häufig zur Lösung anspruchsvoller Optimierungsprobleme mit Nebenbedingungen eingesetzt. Darüber hinaus wird die Methode der Lagrange-Multiplikatoren durch die Karush-Kuhn-Tucker-Bedingungen verallgemeinert, die auch Ungleichheitsbedingungen der folgenden Form berücksichtigen können $h(\mathbf {x} )\leq c$ für eine gegebene Konstante $c$. ⓘ

Visualisierung der Methode der Lagrange-Multiplikatoren. Die rote Linie stellt die Menge dar, auf der $g(x,y)=c$ erfüllt ist. Die blauen Linien sind Höhenlinien $f(x,y)=d$ für verschiedene Werte von $d$. An dem Punkt, an dem $f$ unter der Nebenbedingung $g=c$ maximal ist, verläuft $g=c$ tangential zur Höhenlinie $f(x,y)=d_{1}$. Dort sind die Gradienten der Funktionen $f$ und $g$, dargestellt durch blaue bzw. rote Pfeile, kollinear. ⓘ

Dasselbe Problem wie oben, wobei die Funktionswerte von $f$ auf der Höhenachse abgetragen sind. ⓘ

Aussage

Der folgende Satz ist als Lagrange-Multiplikator-Theorem bekannt. ⓘ

Sei $f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R}$ sei die Zielfunktion, $g\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{c}$ sei die Nebenbedingungsfunktion, beide gehören zu $C^{1}$ (d.h. mit stetigen ersten Ableitungen). Sei $x^{*}$ sei eine optimale Lösung des folgenden Optimierungsproblems, so dass $\operatorname {rank} (Dg(x^{*}))=c<n$ (hier $Dg(x^{*})$ die Matrix der partiellen Ableitungen bezeichnet, ${\textstyle \left[{\partial g_{j}}/{\partial x_{k}}\right]}$):

${\text{maximize}}\ f(x)$

${\text{subject to:}}\ g(x)=0$ ⓘ

Dann gibt es einen einzigen Lagrange-Multiplikator $\lambda ^{*}\in \mathbb {R} ^{c}$ derart, dass $Df(x^{*})=\lambda ^{*T}Dg(x^{*})$. ⓘ

Der Satz vom Lagrange-Multiplikator besagt, dass bei jedem lokalen Maximum (oder Minimum) der Funktion, die unter den Gleichheitsbedingungen ausgewertet wird, der Gradient der Funktion (an diesem Punkt) als Linearkombination der Gradienten der Bedingungen (an diesem Punkt) ausgedrückt werden kann, wobei die Lagrange-Multiplikatoren als Koeffizienten fungieren, wenn die Bedingungsqualifikation gilt (siehe unten). Dies ist gleichbedeutend mit der Aussage, dass jede Richtung, die senkrecht zu allen Steigungen der Nebenbedingungen steht, auch senkrecht zur Steigung der Funktion steht. Oder auch, dass die Richtungsableitung der Funktion in jeder machbaren Richtung 0 ist. ⓘ

Einzelne Nebenbedingung

Abbildung 1: Die rote Kurve zeigt die Nebenbedingung g(x, y) = c. Die blauen Kurven sind die Konturen von f(x, y). Der Punkt, an dem die rote Nebenbedingung tangential eine blaue Kontur berührt, ist das Maximum von f(x, y) entlang der Nebenbedingung, da d₁ > d₂. ⓘ

Für den Fall, dass es nur eine Zwangsbedingung und nur zwei Auswahlvariablen gibt (wie in Abbildung 1 dargestellt), betrachten wir das Optimierungsproblem ⓘ

${\text{maximize}}\ f(x,y)$

${\text{subject to:}}\ g(x,y)=0$ ⓘ

(Manchmal wird eine additive Konstante gesondert dargestellt, anstatt sie in $g$enthalten ist. In diesem Fall wird die Nebenbedingung wie folgt geschrieben $g(x,y)=c$geschrieben, wie in Abbildung 1.) Wir nehmen an, dass sowohl $f$ und $g$ kontinuierliche erste partielle Ableitungen haben. Wir führen eine neue Variable ($\lambda$) ein, die als Lagrange-Multiplikator (oder unbestimmter Lagrange-Multiplikator) bezeichnet wird, und untersuchen die Lagrange-Funktion (oder Lagrangesche Funktion oder Lagrangescher Ausdruck), die durch ⓘ

${\mathcal {L}}(x,y,\lambda )=f(x,y)-\lambda g(x,y),$ ⓘ

wobei der $\lambda$ Term entweder addiert oder subtrahiert werden kann. Wenn $f(x_{0},y_{0})$ ein Maximum von $f(x,y)$ für das ursprüngliche eingeschränkte Problem und $\nabla g(x_{0},y_{0})\neq 0$ist, dann gibt es $\lambda _{0}$ derart, dass ($x_{0},y_{0},\lambda _{0}$) ein stationärer Punkt für die Lagrange-Funktion ist (stationäre Punkte sind die Punkte, in denen die ersten partiellen Ableitungen von ${\mathcal {L}}$ Null sind). Die Annahme $\nabla g\neq 0$ wird Constraint-Qualifikation genannt. Allerdings führen nicht alle stationären Punkte zu einer Lösung des ursprünglichen Problems, da die Methode der Lagrange-Multiplikatoren nur eine notwendige Bedingung für die Optimalität bei Problemen mit Nebenbedingungen liefert. Es gibt auch hinreichende Bedingungen für ein Minimum oder Maximum, aber wenn ein bestimmter Lösungskandidat die hinreichenden Bedingungen erfüllt, ist nur gewährleistet, dass diese Lösung lokal die beste ist, d. h. besser als alle zulässigen Punkte in der Nähe. Das globale Optimum kann durch den Vergleich der Werte der ursprünglichen Zielfunktion an den Punkten gefunden werden, die die notwendigen und lokal ausreichenden Bedingungen erfüllen. ⓘ

Die Methode der Lagrange-Multiplikatoren beruht auf der Intuition, dass f(x, y) bei einem Maximum nicht in Richtung eines solchen Nachbarpunktes ansteigen kann, der ebenfalls g = 0 hat. Wenn dies der Fall wäre, könnte man entlang g = 0 gehen, um höher zu kommen, was bedeutet, dass der Ausgangspunkt nicht wirklich das Maximum war. So gesehen ist es ein exaktes Analogon zur Prüfung, ob die Ableitung einer unbeschränkten Funktion 0 ist, d. h. wir prüfen, ob die Richtungsableitung in jeder relevanten (brauchbaren) Richtung 0 ist. ⓘ

Wir können uns die Konturen von f, gegeben durch f(x, y) = d für verschiedene Werte von d, und die Kontur von g, gegeben durch g(x, y) = c, vorstellen. ⓘ

Angenommen, wir gehen entlang der Konturlinie mit g = c. Wir sind daran interessiert, Punkte zu finden, an denen sich f beim Gehen fast nicht ändert, da diese Punkte Maxima sein könnten. ⓘ

Es gibt zwei Möglichkeiten, wie dies geschehen kann:

1. Wir könnten eine Konturlinie von f berühren, da sich f per Definition nicht ändert, wenn wir entlang seiner Konturlinien gehen. Das würde bedeuten, dass die Tangenten an die Umrisslinien von f und g hier parallel sind.
2. Wir haben einen "ebenen" Teil von f erreicht, was bedeutet, dass sich f in keiner Richtung ändert. ⓘ

Um die erste Möglichkeit zu prüfen (wir berühren eine Höhenlinie von f), ist zu beachten, dass die Tangenten an die Höhenlinien von f und g nur dann parallel sind, wenn die Steigungen von f und g parallel sind, da die Steigung einer Funktion senkrecht zu den Höhenlinien steht. Gesucht sind also Punkte (x, y), in denen g(x, y) = c und ⓘ

$\nabla _{x,y}f=\lambda \,\nabla _{x,y}g,$ ⓘ

für einige $\lambda$ ⓘ

wobei ⓘ

$\nabla _{x,y}f=\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}}\right),\qquad \nabla _{x,y}g=\left({\frac {\partial g}{\partial x}},{\frac {\partial g}{\partial y}}\right)$ ⓘ

die jeweiligen Steigungen sind. Die Konstante $\lambda$ ist erforderlich, weil die beiden Gradientenvektoren zwar parallel sind, aber im Allgemeinen nicht gleich groß sind. Diese Konstante wird als Lagrange-Multiplikator bezeichnet. (In manchen Konventionen wird $\lambda$ wird ein Minuszeichen vorangestellt). ⓘ

Beachten Sie, dass diese Methode auch die zweite Möglichkeit, dass f gleich ist, löst: Wenn f gleich ist, dann ist sein Gradient gleich Null, und die Einstellung $\lambda =0$ ist eine Lösung unabhängig von $\nabla _{x,y}g$. ⓘ

Um diese Bedingungen in eine Gleichung einzubeziehen, führen wir eine Hilfsfunktion ⓘ

${\mathcal {L}}(x,y,\lambda )=f(x,y)-\lambda g(x,y),$ ⓘ

und lösen ⓘ

$\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )=0.$ ⓘ

Man beachte, dass dies auf die Lösung von drei Gleichungen mit drei Unbekannten hinausläuft. Dies ist die Methode der Lagrange-Multiplikatoren. ⓘ

Beachten Sie, dass $\nabla _{\lambda }{\mathcal {L}}(x,y,\lambda )=0$ impliziert $g(x,y)=0$als die partielle Ableitung von ${\mathcal {L}}$ in Bezug auf $\lambda$ ist. $-g(x,y)$ist, die eindeutig Null ist, wenn und nur wenn $g(x,y)=0$. ⓘ

Zusammenfassend

$\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )=0\iff {\begin{cases}\nabla _{x,y}f(x,y)=\lambda \,\nabla _{x,y}g(x,y)\\g(x,y)=0\end{cases}}$ ⓘ

Die Methode lässt sich ohne weiteres auf Funktionen nach $n$ Variablen ⓘ

$\nabla _{x_{1},\dots ,x_{n},\lambda }{\mathcal {L}}(x_{1},\dots ,x_{n},\lambda )=0$ ⓘ

was auf die Lösung von n + 1 Gleichungen in n + 1 Unbekannten hinausläuft. ⓘ

Die eingeschränkten Extrema von f sind kritische Punkte der Lagrange ${\mathcal {L}}$, aber sie sind nicht unbedingt lokale Extrema von ${\mathcal {L}}$ (siehe Beispiel 2 unten). ⓘ

Man kann die Lagrange als einen Hamiltonian umformulieren, in diesem Fall sind die Lösungen lokale Minima für den Hamiltonian. Dies wird in der Theorie der optimalen Steuerung in Form des Pontryaginschen Minimalprinzips getan. ⓘ

Die Tatsache, dass die Lösungen der Lagrange nicht notwendigerweise Extrema sind, bringt auch Schwierigkeiten für die numerische Optimierung mit sich. Dies kann durch die Berechnung des Betrags des Gradienten gelöst werden, da die Nullstellen des Betrags notwendigerweise lokale Minima sind, wie im Beispiel der numerischen Optimierung dargestellt. ⓘ

Mehrere Nebenbedingungen

Abbildung 2: Ein Paraboloid, das an zwei sich schneidende Linien gebunden ist. ⓘ

Abbildung 3: Konturenkarte von Abbildung 2. ⓘ

Die Methode der Lagrange-Multiplikatoren kann mit einer ähnlichen Argumentation auf die Lösung von Problemen mit mehreren Nebenbedingungen erweitert werden. Betrachten wir ein Paraboloid, das zwei Linienzwängen unterliegt, die sich in einem einzigen Punkt schneiden. Da dieser Punkt die einzige machbare Lösung ist, handelt es sich offensichtlich um ein eingeschränktes Extremum. Allerdings ist die Ebenenmenge von $f$ ist jedoch eindeutig nicht parallel zu einer der beiden Nebenbedingungen im Schnittpunkt (siehe Abbildung 3); stattdessen ist sie eine lineare Kombination der Gradienten der beiden Nebenbedingungen. Im Falle mehrerer Nebenbedingungen ist dies das, was wir im Allgemeinen suchen: Die Lagrange-Methode sucht nach Punkten, an denen die Steigung von $f$ nicht notwendigerweise ein Vielfaches der Steigung einer einzelnen Nebenbedingung ist, sondern eine Linearkombination der Steigungen aller Nebenbedingungen darstellt. ⓘ

Konkret: Angenommen, wir haben $M$ Nebenbedingungen und wandern entlang der Menge der Punkte, die folgende Bedingungen erfüllen $g_{i}(\mathbf {x} )=0,i=1,\dots ,M$. Jeder Punkt $\mathbf {x}$ auf der Kontur einer gegebenen Nebenbedingungsfunktion $g_{i}$ hat einen Raum zulässiger Richtungen: den Raum der Vektoren, die senkrecht zu $\nabla g_{i}(\mathbf {x} )$. Die Menge der Richtungen, die für alle Nebenbedingungen zulässig sind, ist somit der Raum der Richtungen, die senkrecht zu allen Gradienten der Nebenbedingungen stehen. Bezeichnen Sie diesen Raum der zulässigen Bewegungen mit $A$ und bezeichne die Spanne der Gradienten der Nebenbedingungen mit $S$. Dann $A=S^{\perp }$der Raum der Vektoren, die senkrecht zu jedem Element von $S$. ⓘ

Wir sind immer noch daran interessiert, Punkte zu finden, bei denen $f$ sich beim Gehen nicht ändert, da es sich bei diesen Punkten um (eingeschränkte) Extrema handeln könnte. Wir suchen daher $\mathbf {x}$ so, dass jede zulässige Bewegungsrichtung weg von $\mathbf {x}$ senkrecht ist zu $\nabla f(\mathbf {x} )$ (andernfalls könnten wir $f$ durch Bewegung entlang dieser zulässigen Richtung). Mit anderen Worten, $\nabla f(\mathbf {x} )\in A^{\perp }=S$. Es gibt also Skalare $\lambda _{1},\lambda _{2},....\lambda _{M}$ derart, dass ⓘ

$\nabla f(\mathbf {x} )=\sum _{k=1}^{M}\lambda _{k}\,\nabla g_{k}(\mathbf {x} )\quad \iff \quad \nabla f(\mathbf {x} )-\sum _{k=1}^{M}{\lambda _{k}\nabla g_{k}(\mathbf {x} )}=0.$ ⓘ

Diese Skalare sind die Lagrange-Multiplikatoren. Wir haben nun $M$ von ihnen, einen für jede Nebenbedingung. ⓘ

Wie zuvor führen wir eine Hilfsfunktion ⓘ

${\mathcal {L}}\left(x_{1},\ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{M}\right)=f\left(x_{1},\ldots ,x_{n}\right)-\sum \limits _{k=1}^{M}{\lambda _{k}g_{k}\left(x_{1},\ldots ,x_{n}\right)}$ ⓘ

und lösen ⓘ

$\nabla _{x_{1},\ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{M}}{\mathcal {L}}(x_{1},\ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{M})=0\iff {\begin{cases}\nabla f(\mathbf {x} )-\sum _{k=1}^{M}{\lambda _{k}\,\nabla g_{k}(\mathbf {x} )}=0\\g_{1}(\mathbf {x} )=\cdots =g_{M}(\mathbf {x} )=0\end{cases}}$ ⓘ

die darauf hinausläuft, dass wir die $n+M$ Gleichungen in $n+M$ Unbekannten. ⓘ

Bei mehreren Nebenbedingungen wird angenommen, dass die Gradienten der Nebenbedingungen an dem betreffenden Punkt linear unabhängig sind. ⓘ

Moderne Formulierung über differenzierbare Mannigfaltigkeiten

Das Problem der Suche nach lokalen Maxima und Minima unter Nebenbedingungen kann verallgemeinert werden auf die Suche nach lokalen Maxima und Minima auf einer differenzierbaren Mannigfaltigkeit $M$. Im Folgenden ist es nicht notwendig, dass $M$ ein euklidischer Raum oder sogar eine Riemannsche Mannigfaltigkeit sein. Alle Erscheinungen des Gradienten $\nabla$ (die von der Wahl der riemannschen Metrik abhängt) kann durch die äußere Ableitung ersetzt werden $d$. ⓘ

Einzelne Nebenbedingung

Sei $M$ sei eine glatte Mannigfaltigkeit der Dimension $m$. Angenommen, wir wollen die stationären Punkte finden $x$ einer glatten Funktion $f:M\to \mathbb {R}$ bei Beschränkung auf die Unterverzweigung $N$ definiert durch $g(x)=0,$ wobei $g:M\to \mathbb {R}$ ist eine glatte Funktion, für die 0 ein regulärer Wert ist. ⓘ

Sei $df$ und $dg$ seien die äußeren Ableitungen. Stationarität für die Einschränkung $f|_{N}$ auf $x\in N$ bedeutet $d(f|_{N})_{x}=0.$ Äquivalent dazu enthält der Kernel $\ker(df_{x})$ enthält $T_{x}N=\ker(dg_{x}).$ Mit anderen Worten, $df_{x}$ und $dg_{x}$ sind proportionale 1-Formen. Dazu ist es notwendig und hinreichend, dass das folgende System von $m(m-1)/2$ Gleichungen gilt:

$df_{x}\wedge dg_{x}=0\in \Lambda ^{2}(T_{x}^{*}M)$ ⓘ

wobei $\wedge$ bezeichnet das äußere Produkt. Die stationären Punkte $x$ sind die Lösungen des obigen Gleichungssystems plus der Nebenbedingung $g(x)=0.$ Man beachte, dass die ${\tfrac {1}{2}}m(m-1)$ Gleichungen nicht unabhängig sind, da die linke Seite der Gleichung zu der Untermenge von $\Lambda ^{2}(T_{x}^{*}M)$ gehört, die aus zersetzbaren Elementen besteht. ⓘ

Bei dieser Formulierung ist es nicht notwendig, den Lagrange-Multiplikator explizit zu bestimmen, eine Zahl $\lambda$ derart, dass $df_{x}=\lambda \,dg_{x}.$ ⓘ

Mehrere Nebenbedingungen

Sei $M$ und $f$ zu finden, wie im obigen Abschnitt für den Fall einer einzigen Zwangsbedingung. Anstelle der dort beschriebenen Funktion $g$ betrachten wir nun eine glatte Funktion $G:M\to \mathbb {R} ^{p}(p>1),$ mit Komponentenfunktionen $g_{i}:M\to \mathbb {R} ,$ für die $0\in \mathbb {R} ^{p}$ ein regulärer Wert ist. Sei $N$ sei die Untermannigfaltigkeit von $M$ definiert durch $G(x)=0.$ ⓘ

$x$ ist ein stationärer Punkt von $f|_{N}$ wenn und nur wenn $\ker(df_{x})$ enthält $\ker(dG_{x})$. Der Einfachheit halber sei $L_{x}=df_{x}$ und $K_{x}=dG_{x},$ wobei $dG$ die Tangentenkarte oder die Jacobikarte $TM\to T\mathbb {R} ^{p}.$ Der Unterraum $\ker(K_{x})$ hat eine kleinere Dimension als die von $\ker(L_{x})$, nämlich $\dim(\ker(L_{x}))=n-1$ und $\dim(\ker(K_{x}))=n-p.$ $\ker(K_{x})$ gehört zu $\ker(L_{x})$ wenn und nur wenn $L_{x}\in T_{x}^{*}M$ gehört zu dem Bild von $K_{x}^{*}:\mathbb {R} ^{p*}\to T_{x}^{*}M.$ Rechnerisch gesehen ist die Bedingung, dass $L_{x}$ zum Zeilenraum der Matrix von $K_{x},$ oder äquivalent dazu dem Spaltenraum der Matrix von $K_{x}^{*}$ (die Transponierte). Wenn $\omega _{x}\in \Lambda ^{p}(T_{x}^{*}M)$ das äußere Produkt der Spalten der Matrix von $K_{x}^{*},$ bezeichnet, ist die stationäre Bedingung für $f|_{N}$ auf $x$ zu ⓘ

$L_{x}\wedge \omega _{x}=0\in \Lambda ^{p+1}\left(T_{x}^{*}M\right)$ ⓘ

Auch bei dieser Formulierung ist es nicht notwendig, die Lagrange-Multiplikatoren explizit zu bestimmen, da die Zahlen $\lambda _{1},\ldots ,\lambda _{p}$ derart, dass ⓘ

$df_{x}=\sum _{i=1}^{p}\lambda _{i}d(g_{i})_{x}.$ ⓘ

Interpretation der Lagrange-Multiplikatoren

Oftmals werden die Lagrange-Multiplikatoren als eine interessierende Größe interpretiert. Zum Beispiel durch Parametrisierung der Konturlinie der Zwangsbedingung, das heißt, wenn der Lagrange-Ausdruck ⓘ

${\begin{aligned}&{\mathcal {L}}(x_{1},x_{2},\ldots ;\lambda _{1},\lambda _{2},\ldots ;c_{1},c_{2},\ldots )\\[4pt]={}&f(x_{1},x_{2},\ldots )+\lambda _{1}(c_{1}-g_{1}(x_{1},x_{2},\ldots ))+\lambda _{2}(c_{2}-g_{2}(x_{1},x_{2},\dots ))+\cdots \end{aligned}}$ ⓘ

dann ⓘ

${\frac {\partial {\mathcal {L}}}{\partial c_{k}}}=\lambda _{k}.$ ⓘ

λk ist also die Änderungsrate der zu optimierenden Größe in Abhängigkeit vom Parameter der Nebenbedingung. In der Lagrangeschen Mechanik werden die Bewegungsgleichungen beispielsweise durch die Suche nach stationären Punkten der Aktion, dem Zeitintegral der Differenz zwischen kinetischer und potentieller Energie, abgeleitet. So kann die Kraft, die auf ein Teilchen aufgrund eines skalaren Potenzials wirkt, F = -∇V, als Lagrange-Multiplikator interpretiert werden, der die Änderung der Wirkung (Übertragung von potenzieller in kinetische Energie) infolge einer Änderung der eingeschränkten Flugbahn des Teilchens bestimmt. In der Steuerungstheorie wird dies stattdessen als Kostengleichungen formuliert. ⓘ

Darüber hinaus lässt sich der optimale Wert eines Lagrange-Multiplikators nach dem Hüllkurvensatz als die marginale Auswirkung der entsprechenden Randbedingungskonstante auf den optimal erreichbaren Wert der ursprünglichen Zielfunktion interpretieren: Wenn wir die Werte am Optimum mit einem Sternchen kennzeichnen, dann lässt sich zeigen, dass ⓘ

${\frac {{\text{d}}f(x_{1}^{*}(c_{1},c_{2},\dots ),x_{2}^{*}(c_{1},c_{2},\dots ),\dots )}{{\text{d}}c_{k}}}=\lambda _{k}^{*}.$ ⓘ

In den Wirtschaftswissenschaften wird beispielsweise der optimale Gewinn eines Spielers unter Berücksichtigung eines beschränkten Handlungsraums berechnet, wobei ein Lagrange-Multiplikator die Änderung des optimalen Werts der Zielfunktion (Gewinn) aufgrund der Lockerung einer bestimmten Beschränkung (z. B. durch eine Änderung des Einkommens) ist; in einem solchen Zusammenhang ist λk* die Grenzkosten der Beschränkung und wird als Schattenpreis bezeichnet. ⓘ

Hinreichende Bedingungen

Dieses Verfahren liefert nur eine notwendige Bedingung für Extremstellen. Um die Extremstellen nachzuweisen und ihre Art zu bestimmen, gibt es verschiedene Kriterien. Generell wird die geränderte Hesse-Matrix gebildet und deren Determinante bzw. bestimmte Unterdeterminanten berechnet. Dieser Ansatz führt aber nicht immer zu einer Aussage. Alternativ kann man auch auf eine Visualisierung bzw. geometrische Überlegungen zurückgreifen, um die Art der Extremstelle festzustellen. ⓘ

Hinreichende Bedingungen für ein beschränktes lokales Maximum oder Minimum können in Form einer Folge von Hauptminoren (Determinanten von links oben justierten Teilmatrizen) der begrenzten Hess'schen Matrix der zweiten Ableitungen des Lagrange-Ausdrucks angegeben werden. ⓘ

Beispiele

Beispiel 1

Darstellung eines Optimierungsproblems mit einer Nebenbedingung ⓘ

Veranschaulichung des eingeschränkten Optimierungsproblems 1a ⓘ

Beispiel 1a

Angenommen, wir wollen maximieren $f(x,y)=x+y$ unter Berücksichtigung der Nebenbedingung $x^{2}+y^{2}=1$. Die machbare Menge ist der Einheitskreis, und die Ebenenmengen von f sind diagonale Linien (mit der Steigung -1), so dass wir grafisch sehen können, dass das Maximum bei $\left({\tfrac {1}{\sqrt {2}}},{\tfrac {1}{\sqrt {2}}}\right)$und das Minimum bei $\left(-{\tfrac {1}{\sqrt {2}}},-{\tfrac {1}{\sqrt {2}}}\right)$. ⓘ

Bei der Methode der Lagrange-Multiplikatoren ist die Nebenbedingung ⓘ

$g(x,y)=x^{2}+y^{2}-1=0,$ ⓘ

also die Lagrangesche Funktion, ⓘ

${\begin{aligned}{\mathcal {L}}(x,y,\lambda )&=f(x,y)+\lambda \cdot g(x,y)\\[4pt]&=x+y+\lambda (x^{2}+y^{2}-1),\end{aligned}}$ ⓘ

ist eine Funktion, die äquivalent ist zu $f(x,y)$ wenn $g(x,y)$ gesetzt wird zu $0$. ⓘ

Jetzt können wir den Gradienten berechnen:

${\begin{aligned}\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )&=\left({\frac {\partial {\mathcal {L}}}{\partial x}},{\frac {\partial {\mathcal {L}}}{\partial y}},{\frac {\partial {\mathcal {L}}}{\partial \lambda }}\right)\\[4pt]&=\left(1+2\lambda x,1+2\lambda y,x^{2}+y^{2}-1\right)\,\color {gray}{,}\end{aligned}}$ ⓘ

und daher:

$\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )=0\quad \Leftrightarrow \quad {\begin{cases}1+2\lambda x=0\\1+2\lambda y=0\\x^{2}+y^{2}-1=0\end{cases}}$ ⓘ

Beachten Sie, dass die letzte Gleichung die ursprüngliche Zwangsbedingung ist. ⓘ

Die ersten beiden Gleichungen ergeben ⓘ

$x=y=-{\frac {1}{2\lambda }},\qquad \lambda \neq 0.$ ⓘ

Durch Einsetzen in die letzte Gleichung erhalten wir:

${\frac {1}{4\lambda ^{2}}}+{\frac {1}{4\lambda ^{2}}}-1=0,$ ⓘ

also ⓘ

$\lambda =\pm {\frac {1}{\sqrt {2}}},$ ⓘ

was bedeutet, dass die stationären Punkte von ${\mathcal {L}}$ sind. ⓘ

$\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}},-{\tfrac {1}{\sqrt {2}}}\right),\qquad \left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}},{\tfrac {1}{\sqrt {2}}}\right).$ ⓘ

Die Auswertung der Zielfunktion f an diesen Punkten ergibt ⓘ

$f\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right)={\sqrt {2}},\qquad f\left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)=-{\sqrt {2}}.$ ⓘ

Das eingeschränkte Maximum ist also ${\sqrt {2}}$ und das eingeschränkte Minimum ist $-{\sqrt {2}}$. ⓘ

Beispiel 1b

Illustration des eingeschränkten Optimierungsproblems 1b ⓘ

Nun modifizieren wir die Zielfunktion von Beispiel 1a so, dass wir minimieren $f(x,y)=(x+y)^{2}$ anstelle von $f(x,y)=x+y,$ wieder entlang des Kreises $g(x,y)=x^{2}+y^{2}-1=0$. Nun sind die Ebenenmengen von $f$ sind immer noch Geraden mit der Steigung -1, und die Punkte auf dem Kreis, die diese Ebenen tangieren, sind wieder $({\sqrt {2}}/2,{\sqrt {2}}/2)$ und $(-{\sqrt {2}}/2,-{\sqrt {2}}/2)$. Diese Berührungspunkte sind Maxima von $f$. ⓘ

Andererseits treten die Minima auf der Ebenenmenge für $f$ = 0 (da aufgrund seiner Konstruktion $f$ keine negativen Werte annehmen kann), bei $({\sqrt {2}}/2,-{\sqrt {2}}/2)$ und $(-{\sqrt {2}}/2,{\sqrt {2}}/2)$, wo die Niveaukurven von $f$ nicht tangential zur Nebenbedingung sind. Die Bedingung, die $\nabla _{x,y,\lambda }\left(f(x,y)+\lambda \cdot g(x,y)\right)=0$ identifiziert alle vier Punkte korrekt als Extrema; die Minima sind in gekennzeichnet durch $\lambda =0$ und die Maxima durch $\lambda =-2$. ⓘ

Beispiel 2

Veranschaulichung des Problems der eingeschränkten Optimierung ⓘ

In diesem Beispiel geht es um anspruchsvollere Berechnungen, aber es handelt sich immer noch um ein Problem mit einer einzigen Nebenbedingung. ⓘ

Angenommen, man möchte die Maximalwerte von ⓘ

$f(x,y)=x^{2}y$ ⓘ

mit der Bedingung, dass die $x$- und $y$-Koordinaten auf einem Kreis um den Ursprung mit dem Radius ${\sqrt {3}}$. Das heißt, es gilt die Bedingung ⓘ

$g(x,y)=x^{2}+y^{2}-3=0.$ ⓘ

Da es nur eine einzige Nebenbedingung gibt, gibt es auch nur einen einzigen Multiplikator, nämlich $\lambda$. ⓘ

Die Nebenbedingung $g(x,y)$ ist identisch Null auf dem Kreis mit Radius ${\sqrt {3}}$. Jedes Vielfache von $g(x,y)$ kann addiert werden zu $g(x,y)$ wobei $g(x,y)$ in der interessierenden Region (auf dem Kreis, auf dem unsere ursprüngliche Bedingung erfüllt ist) unverändert bleibt. ⓘ

Die Anwendung der gewöhnlichen Lagrange-Multiplikator-Methode ergibt ⓘ

${\begin{aligned}{\mathcal {L}}(x,y,\lambda )&=f(x,y)+\lambda \cdot g(x,y)\\&=x^{2}y+\lambda (x^{2}+y^{2}-3),\end{aligned}}$ ⓘ

woraus der Gradient berechnet werden kann:

${\begin{aligned}\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )&=\left({\frac {\partial {\mathcal {L}}}{\partial x}},{\frac {\partial {\mathcal {L}}}{\partial y}},{\frac {\partial {\mathcal {L}}}{\partial \lambda }}\right)\\&=\left(2xy+2\lambda x,x^{2}+2\lambda y,x^{2}+y^{2}-3\right).\end{aligned}}$ ⓘ

Und deshalb:

$\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )=0\quad \iff \quad {\begin{cases}2xy+2\lambda x=0\\x^{2}+2\lambda y=0\\x^{2}+y^{2}-3=0\end{cases}}\quad \iff \quad {\begin{cases}x(y+\lambda )=0&{\text{(i)}}\\x^{2}=-2\lambda y&{\text{(ii)}}\\x^{2}+y^{2}=3&{\text{(iii)}}\end{cases}}$ ⓘ

(iii) ist nur die ursprüngliche Randbedingung. (i) impliziert $x=0$ oder $\lambda =-y$. Wenn $x=0$ dann $y=\pm {\sqrt {3}}$ durch (iii) und folglich $\lambda =0$ aus (ii). Wenn $\lambda =-y$in (ii) eingesetzt wird, ergibt sich $x^{2}=2y^{2}$. Setzt man dies in (iii) ein und löst für $y$ ergibt $y=\pm 1$. Es gibt also sechs kritische Punkte von ${\mathcal {L}}$:

$({\sqrt {2}},1,-1);\quad (-{\sqrt {2}},1,-1);\quad ({\sqrt {2}},-1,1);\quad (-{\sqrt {2}},-1,1);\quad (0,{\sqrt {3}},0);\quad (0,-{\sqrt {3}},0).$ ⓘ

Bewertet man die Zielfunktion an diesen Punkten, so erhält man ⓘ

$f(\pm {\sqrt {2}},1)=2;\quad f(\pm {\sqrt {2}},-1)=-2;\quad f(0,\pm {\sqrt {3}})=0.$ ⓘ

Daher erreicht die Zielfunktion das globale Maximum (unter Berücksichtigung der Nebenbedingungen) bei $(\pm {\sqrt {2}},1)$ und das globale Minimum bei $(\pm {\sqrt {2}},-1).$ Der Punkt $(0,{\sqrt {3}})$ ist ein lokales Minimum von $f$ und $(0,-{\sqrt {3}})$ ist ein lokales Maximum von $f$wie durch Betrachtung der Hessischen Matrix von ${\mathcal {L}}(x,y,0)$. ⓘ

Man beachte, dass, während $({\sqrt {2}},1,-1)$ ein kritischer Punkt von ${\mathcal {L}}$ist, ist es kein lokales Extremum von ${\mathcal {L}}.$ Wir haben ⓘ

${\mathcal {L}}\left({\sqrt {2}}+\varepsilon ,1,-1+\delta \right)=2+\delta \left(\varepsilon ^{2}+\left(2{\sqrt {2}}\right)\varepsilon \right).$ ⓘ

Bei einer beliebigen Nachbarschaft von $({\sqrt {2}},1,-1)$kann man ein kleines positives $\varepsilon$ und ein kleines $\delta$ mit beliebigem Vorzeichen wählen, um ${\mathcal {L}}$ Werte sowohl größer als auch kleiner als $2$. Dies lässt sich auch aus der Hessischen Matrix von ${\mathcal {L}}$ die an diesem Punkt (oder an jedem der kritischen Punkte) ausgewertet wird, die eine unbestimmte Matrix ist. Jeder der kritischen Punkte von ${\mathcal {L}}$ ist ein Sattelpunkt von ${\mathcal {L}}$. ⓘ

Beispiel 3: Entropie

Angenommen, wir wollen die diskrete Wahrscheinlichkeitsverteilung in den Punkten $\{p_{1},p_{2},\ldots ,p_{n}\}$ mit maximaler Informationsentropie finden. Dies ist dasselbe wie die Suche nach der am wenigsten strukturierten Wahrscheinlichkeitsverteilung in den Punkten $\{p_{1},p_{2},\cdots ,p_{n}\}$. Mit anderen Worten, wir wollen die Shannon-Entropie-Gleichung maximieren:

$f(p_{1},p_{2},\ldots ,p_{n})=-\sum _{j=1}^{n}p_{j}\log _{2}p_{j}.$ ⓘ

Damit dies eine Wahrscheinlichkeitsverteilung ist, muss die Summe der Wahrscheinlichkeiten $p_{i}$ an jedem Punkt $x_{i}$ gleich 1 sein, also lautet unsere Bedingung:

$g(p_{1},p_{2},\ldots ,p_{n})=\sum _{j=1}^{n}p_{j}=1.$ ⓘ

Wir verwenden Lagrange-Multiplikatoren, um den Punkt der maximalen Entropie zu finden, ${\vec {p}}^{\,*}$über alle diskreten Wahrscheinlichkeitsverteilungen ${\vec {p}}$ auf $\{x_{1},x_{2},\ldots ,x_{n}\}$. Wir verlangen, dass:

$\left.{\frac {\partial }{\partial {\vec {p}}}}(f+\lambda (g-1))\right|_{{\vec {p}}={\vec {p}}^{\,*}}=0,$ ⓘ

was ein System von n Gleichungen ergibt, $k=1,\ldots ,n$, so dass:

$\left.{\frac {\partial }{\partial p_{k}}}\left\{-\left(\sum _{j=1}^{n}p_{j}\log _{2}p_{j}\right)+\lambda \left(\sum _{j=1}^{n}p_{j}-1\right)\right\}\right|_{p_{k}=p_{k}^{*}}=0.$ ⓘ

Wenn wir die Differenzierung dieser n Gleichungen durchführen, erhalten wir ⓘ

$-\left({\frac {1}{\ln 2}}+\log _{2}p_{k}^{*}\right)+\lambda =0.$ ⓘ

Dies zeigt, dass alle $p_{k}^{*}$ gleich sind (weil sie nur von λ abhängen). Durch die Anwendung der Nebenbedingung ⓘ

$\sum _{j}p_{j}=1,$ ⓘ

finden wir ⓘ

$p_{k}^{*}={\frac {1}{n}}.$ ⓘ

Die Gleichverteilung ist also die Verteilung mit der größten Entropie unter den Verteilungen auf n Punkten. ⓘ

Beispiel 4: Numerische Optimierung

Die Lagrange-Multiplikatoren bewirken, dass die kritischen Punkte an Sattelpunkten auftreten. ⓘ

Die Größe des Gradienten kann verwendet werden, um die kritischen Punkte auf lokale Minima zu zwingen. ⓘ

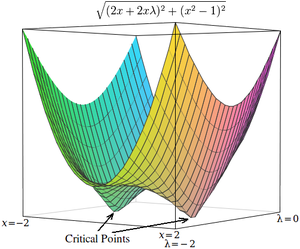
Die kritischen Punkte von Lagrangeschen Multiplikatoren treten an Sattelpunkten auf, nicht an lokalen Maxima (oder Minima). Leider sind viele numerische Optimierungsverfahren wie Hill Climbing, Gradientenabstieg, einige der Quasi-Newton-Methoden und andere darauf ausgelegt, lokale Maxima (oder Minima) und keine Sattelpunkte zu finden. Aus diesem Grund muss man entweder die Formulierung ändern, um sicherzustellen, dass es sich um ein Minimierungsproblem handelt (z. B. durch Extremisierung des Quadrats des Gradienten der Lagrange wie unten), oder eine Optimierungstechnik verwenden, die stationäre Punkte (wie die Newton-Methode ohne extremumssuchende Liniensuche) und nicht unbedingt Extrema findet. ⓘ

Als einfaches Beispiel betrachten wir das Problem, den Wert von x zu finden, der minimiert $f(x)=x^{2}$, mit der Einschränkung, dass $x^{2}=1$. (Dieses Problem ist etwas pathologisch, weil es nur zwei Werte gibt, die diese Bedingung erfüllen, aber es ist zur Veranschaulichung nützlich, weil die entsprechende Funktion ohne Bedingung in drei Dimensionen dargestellt werden kann). ⓘ

Mit Hilfe von Lagrange-Multiplikatoren kann dieses Problem in ein ungebundenes Optimierungsproblem umgewandelt werden:

${\mathcal {L}}(x,\lambda )=x^{2}+\lambda (x^{2}-1).$ ⓘ

Die beiden kritischen Punkte liegen in den Sattelpunkten x = 1 und x = -1. ⓘ

Um dieses Problem mit einem numerischen Optimierungsverfahren zu lösen, müssen wir das Problem zunächst so umformen, dass die kritischen Punkte in lokalen Minima auftreten. Dies geschieht durch die Berechnung der Größe des Gradienten des unbeschränkten Optimierungsproblems. ⓘ

Zunächst berechnen wir die partielle Ableitung des uneingeschränkten Problems nach jeder Variablen:

${\begin{aligned}&{\frac {\partial {\mathcal {L}}}{\partial x}}=2x+2x\lambda \\[5pt]&{\frac {\partial {\mathcal {L}}}{\partial \lambda }}=x^{2}-1.\end{aligned}}$ ⓘ

Wenn die Zielfunktion nicht leicht differenzierbar ist, kann die Ableitung nach jeder Variablen näherungsweise wie folgt berechnet werden ⓘ

${\begin{aligned}{\frac {\partial {\mathcal {L}}}{\partial x}}\approx {\frac {{\mathcal {L}}(x+\varepsilon ,\lambda )-{\mathcal {L}}(x,\lambda )}{\varepsilon }},\\[5pt]{\frac {\partial {\mathcal {L}}}{\partial \lambda }}\approx {\frac {{\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\lambda )}{\varepsilon }},\end{aligned}}$ ⓘ

wobei $\varepsilon$ ein kleiner Wert ist. ⓘ

Als nächstes berechnen wir den Betrag des Gradienten, der die Quadratwurzel aus der Summe der Quadrate der partiellen Ableitungen ist:

${\begin{aligned}h(x,\lambda )&={\sqrt {(2x+2x\lambda )^{2}+(x^{2}-1)^{2}}}\\[4pt]&\approx {\sqrt {\left({\frac {{\mathcal {L}}(x+\varepsilon ,\lambda )-{\mathcal {L}}(x,\lambda )}{\varepsilon }}\right)^{2}+\left({\frac {{\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\lambda )}{\varepsilon }}\right)^{2}}}.\end{aligned}}$ ⓘ

(Da der Betrag immer nicht-negativ ist, ist die Optimierung über den quadrierten Betrag gleichbedeutend mit der Optimierung über den Betrag. Die "Quadratwurzel" kann also in diesen Gleichungen weggelassen werden, ohne dass dies einen Unterschied in den Optimierungsergebnissen zur Folge hätte). ⓘ

Die kritischen Punkte von h treten bei x = 1 und x = -1 auf, genau wie in ${\mathcal {L}}$. Anders als die kritischen Punkte in ${\mathcal {L}}$treten die kritischen Punkte in h jedoch bei lokalen Minima auf, so dass numerische Optimierungstechniken zu ihrer Ermittlung eingesetzt werden können. ⓘ

Anwendungen

Steuerungstheorie

In der Theorie der optimalen Steuerung werden die Lagrange-Multiplikatoren als Kostenvariablen interpretiert, und die Lagrange-Multiplikatoren werden im Pontryagin'schen Minimalprinzip als Minimierung des Hamiltonianers umformuliert. ⓘ

Nichtlineare Programmierung

Die Karush-Kuhn-Tucker-Bedingungen und die Fritz-John-Bedingungen sind eine Verallgemeinerung der Lagrange-Multiplikatoren für Nebenbedingungen, die auch durch Ungleichungen beschrieben werden. Beide spielen eine wichtige Rolle in der nichtlinearen Optimierung. Für konvexe Optimierungsprobleme, bei denen die Funktionen nicht stetig differenzierbar sind, gibt es außerdem die Sattelpunktkriterien der Lagrange-Funktion. ⓘ

Die Methode der Lagrange-Multiplikatoren hat mehrere Verallgemeinerungen. In der nichtlinearen Programmierung gibt es mehrere Multiplikatorregeln, z. B. die Carathéodory-John-Multiplikatorregel und die konvexe Multiplikatorregel für Ungleichheitsrestriktionen. ⓘ

Leistungssysteme

Methoden auf der Grundlage von Lagrange-Multiplikatoren finden Anwendung in Stromversorgungssystemen, z. B. bei der Platzierung verteilter Energieressourcen (DER) und beim Lastabwurf. ⓘ