Box-Plot

Abbildung 1. Boxplot von Daten aus dem Michelson-Experiment ⓘ

In der deskriptiven Statistik ist ein Boxplot eine Methode zur grafischen Darstellung der Lokalisierung, Streuung und Schiefe von numerischen Daten durch ihre Quartile. Zusätzlich zu der Box in einem Boxplot kann es Linien (so genannte Whisker) geben, die sich von der Box aus erstrecken und die Variabilität außerhalb des oberen und unteren Quartils anzeigen; daher wird das Diagramm auch als Box-and-Whisker-Plot oder Box-and-Whisker-Diagramm bezeichnet. Ausreißer, die sich signifikant vom Rest des Datensatzes unterscheiden, können als einzelne Punkte jenseits der Whisker auf dem Box-Plot dargestellt werden. Boxplots sind nichtparametrisch: Sie zeigen die Variation in Stichproben einer statistischen Grundgesamtheit an, ohne Annahmen über die zugrundeliegende statistische Verteilung zu treffen (obwohl Tukey's Boxplot Symmetrie für die Whisker und Normalität für deren Länge voraussetzt). Die Abstände in den einzelnen Unterabschnitten des Boxplots geben den Grad der Streuung und Schiefe der Daten an, die in der Regel mit Hilfe der fünfstelligen Zusammenfassung beschrieben werden. Darüber hinaus ermöglicht das Box-Plot die visuelle Schätzung verschiedener L-Schätzer, insbesondere des Interquartilsbereichs, des mittleren Schenkels, des Bereichs, des mittleren Bereichs und des Trimeans. Boxplots können entweder horizontal oder vertikal gezeichnet werden. ⓘ

Geschichte

Die Range-Bar-Methode wurde erstmals von Mary Eleanor Spear in ihrem Buch "Charting Statistics" (1952) und erneut in ihrem Buch "Practical Charting Techniques" (1969) vorgestellt. Das Box-and-Whisker-Diagramm wurde erstmals 1970 von John Tukey vorgestellt, der später in seinem Buch "Exploratory Data Analysis" (1977) über dieses Thema veröffentlichte. ⓘ

Elemente

Abbildung 2. Box-Plot mit Whiskers vom Minimum zum Maximum ⓘ

Abbildung 3. Gleiches Boxplot mit Whiskern innerhalb des 1,5 IQR-Wertes ⓘ

Ein Boxplot ist eine standardisierte Art der Darstellung des Datensatzes auf der Grundlage der fünfstelligen Zusammenfassung: das Minimum, das Maximum, der Stichprobenmedian und das erste und dritte Quartil. ⓘ

• Minimum (Q₀ oder 0. Perzentil): der niedrigste Datenpunkt im Datensatz ohne Ausreißer
• Maximum (Q₄ oder 100. Perzentil): der höchste Datenpunkt im Datensatz ohne Ausreißer
• Median (Q₂ oder 50. Perzentil): der mittlere Wert des Datensatzes
• Erstes Quartil (Q₁ oder 25. Perzentil): auch bekannt als unteres Quartil qn(0,25), es ist der Median der unteren Hälfte des Datensatzes.
• Drittes Quartil (Q₃ oder 75. Perzentil): auch als oberes Quartil qn(0,75) bezeichnet, es ist der Median der oberen Hälfte des Datensatzes. ⓘ

Zusätzlich zu den Minimal- und Maximalwerten, die zur Erstellung eines Box-Plots verwendet werden, ist ein weiteres wichtiges Element, das ebenfalls zur Erstellung eines Box-Plots verwendet werden kann, der Interquartilsbereich (IQR), wie unten dargestellt:

• Interquartilsbereich (IQR): der Abstand zwischen dem oberen und dem unteren Quartil ⓘ

${\text{IQR}}=Q_{3}-Q_{1}=q_{n}(0.75)-q_{n}(0.25)$ ⓘ

Ein Boxplot besteht in der Regel aus zwei Teilen, einer Box und einer Reihe von Whiskern, wie in Abbildung 2 dargestellt. Die Box wird von Q₁ bis Q₃ mit einer horizontalen Linie in der Mitte gezeichnet, um den Median zu kennzeichnen. Die Whisker können auf verschiedene Weise definiert werden. ⓘ

Bei der einfachsten Methode ist die Begrenzung des unteren Whiskers der Minimalwert des Datensatzes und die Begrenzung des oberen Whiskers der Maximalwert des Datensatzes. ⓘ

Eine weitere beliebte Wahl für die Grenzen der Whisker basiert auf dem 1,5 IQR-Wert. Oberhalb des oberen Quartils (Q₃) wird ein Abstand vom 1,5-fachen des IQR gemessen, und ein Whisker wird bis zum größten beobachteten Datenpunkt des Datensatzes gezogen, der innerhalb dieses Abstands liegt. In ähnlicher Weise wird ein Abstand vom 1,5-fachen des IQR unterhalb des unteren Quartils (Q₁) gemessen und ein Whisker nach unten zum niedrigsten beobachteten Datenpunkt aus dem Datensatz gezogen, der innerhalb dieses Abstands liegt. Da die Whisker an einem beobachteten Datenpunkt enden müssen, können die Whiskerlängen ungleich aussehen, obwohl 1,5 IQR für beide Seiten gleich ist. Alle anderen beobachteten Datenpunkte außerhalb der Whisker-Grenze werden als Ausreißer gezeichnet. Die Ausreißer können auf dem Box-Plot als Punkt, kleiner Kreis, Stern usw. dargestellt werden. ⓘ

Die Whisker können jedoch auch für verschiedene andere Dinge stehen, wie z. B.:

• den Mindest- und den Höchstwert des Datensatzes (wie in Abbildung 2 dargestellt)
• eine Standardabweichung über und unter dem Mittelwert des Datensatzes
• das 9. Perzentil und das 91. Perzentil des Datensatzes
• Das 2. Perzentil und das 98. Perzentil des Datensatzes ⓘ

In seltenen Fällen kann ein Box-Plot auch ohne Whisker gezeichnet werden. ⓘ

Einige Boxplots enthalten ein zusätzliches Zeichen, das den Mittelwert der Daten darstellt. ⓘ

Die ungewöhnlichen Perzentile 2%, 9%, 91%, 98% werden manchmal für Whisker-Kreuzschraffuren und Whisker-Enden verwendet, um die siebenstellige Zusammenfassung darzustellen. Wenn die Daten normalverteilt sind, liegen die sieben Markierungen im Boxplot in gleichen Abständen. Bei einigen Boxplots wird vor dem Ende jedes Whiskers eine Kreuzschraffur gesetzt. ⓘ

Aufgrund dieser Variabilität ist es angebracht, die Konvention, die für die Whisker und Ausreißer verwendet wird, in der Beschriftung des Box-Plots zu beschreiben. ⓘ

Schwankungen

Abbildung 4. Vier Box-Plots, mit und ohne Einkerbungen und variabler Breite ⓘ

Seit der Mathematiker John W. Tukey diese Art der visuellen Datendarstellung 1969 erstmals populär machte, wurden mehrere Variationen des klassischen Box-Plots entwickelt. Die beiden am häufigsten anzutreffenden Varianten sind die Box-Plots mit variabler Breite und die in Abbildung 4 gezeigten Box-Plots mit Einkerbungen. ⓘ

Boxplots mit variabler Breite veranschaulichen die Größe der einzelnen Gruppen, deren Daten aufgezeichnet werden, indem die Breite der Box proportional zur Größe der Gruppe ist. Eine gängige Konvention besteht darin, die Boxbreite proportional zur Quadratwurzel der Gruppengröße zu machen. ⓘ

Bei Notched Box Plots wird eine "Kerbe" oder eine Verengung der Box um den Median herum angebracht. Kerben sind nützlich, um einen groben Anhaltspunkt für die Signifikanz des Unterschieds zwischen den Medianen zu geben; wenn sich die Kerben zweier Boxen nicht überschneiden, ist dies ein Hinweis auf einen statistisch signifikanten Unterschied zwischen den Medianen. Die Breite der Kerben ist proportional zum Interquartilsbereich (IQR) der Stichprobe und umgekehrt proportional zur Quadratwurzel aus der Größe der Stichprobe. Es besteht jedoch Unsicherheit über den am besten geeigneten Multiplikator (da dieser je nach Ähnlichkeit der Varianzen der Stichproben variieren kann). ⓘ

Eine Konvention zur Ermittlung der Grenzen dieser Kerben ist die Verwendung eines Abstands von $\pm {\frac {1.58{\text{ IQR}}}{\sqrt {n}}}$ um den Median. ⓘ

Angepasste Boxplots sollen schiefe Verteilungen beschreiben und beruhen auf der Medcouple-Statistik der Schiefe. Für einen Medcouple-Wert von MC sind die Längen der oberen und unteren Whisker auf dem Box-Plot wie folgt definiert:

${\begin{matrix}1.5{\text{IQR}}\cdot e^{3{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-4{\text{MC}}}{\text{ if }}{\text{MC}}\geq 0,\\1.5{\text{IQR}}\cdot e^{4{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-3{\text{MC}}}{\text{ if }}{\text{MC}}\leq 0.\end{matrix}}$

Bei einer symmetrischen Datenverteilung ist das Medcouple gleich Null, und dies reduziert den angepassten Box-Plot auf den Tukey-Box-Plot mit gleichen Whisker-Längen von $1.5{\text{ IQR}}$ für beide Whisker. ⓘ

Andere Arten von Box-Plots, wie z. B. Violin-Plots und Bean-Plots, können den Unterschied zwischen einmodalen und multimodalen Verteilungen aufzeigen, der im ursprünglichen klassischen Box-Plot nicht zu erkennen ist. ⓘ

Gekerbter Box-Plot für die Größe der Bundesstaaten der USA. ⓘ

Eine Abwandlung besteht darin, das arithmetische Mittel in einen Box-Plot mit einzutragen. Es wird dabei meist als Stern eingetragen. Da der Box-Plot ansonsten nur robuste Streuungs- und Lagemaße enthält, sollte das arithmetische Mittel als nicht-robustes Lagemaß eigentlich nicht in einen Box-Plot aufgenommen werden. ⓘ

Im gekerbten (engl. notched) Box-Plot werden auch Konfidenzintervalle für den Median aufgenommen. ⓘ

Ein Box-Plot besteht immer aus einem Rechteck, genannt Box, und zwei Linien, die dieses Rechteck verlängern. Diese Linien werden als „Antenne“ oder seltener als „Fühler“ oder „Whisker“ bezeichnet und werden durch einen Strich abgeschlossen. In der Regel repräsentiert der Strich in der Box den Median der Verteilung. ⓘ

Beispiele

Beispiel ohne Ausreißer

Abbildung 5. Die generierte Boxplot-Abbildung des Beispiels links ohne Ausreißer. ⓘ

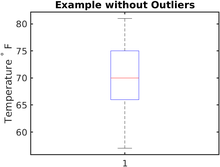
Es wurde eine Reihe von stündlichen Temperaturen in Grad Fahrenheit über den Tag hinweg gemessen. Die aufgezeichneten Werte sind in folgender Reihenfolge aufgeführt (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81. ⓘ

Ein Boxplot des Datensatzes kann erstellt werden, indem zunächst fünf relevante Werte dieses Datensatzes berechnet werden: Minimum, Maximum, Median (Q₂), erstes Quartil (Q₁) und drittes Quartil (Q₃). ⓘ

Das Minimum ist die kleinste Zahl des Datensatzes. In diesem Fall beträgt die niedrigste aufgezeichnete Tagestemperatur 57 °F. ⓘ

Das Maximum ist die größte Zahl des Datensatzes. In diesem Fall beträgt die höchste aufgezeichnete Tagestemperatur 81 °F. ⓘ

Der Median ist die "mittlere" Zahl des geordneten Datensatzes. Das bedeutet, dass genau 50% der Elemente kleiner als der Median und 50% der Elemente größer als der Median sind. Der Median dieses geordneten Datensatzes ist 70 °F. ⓘ

Der erste Quartilswert (Q₁ oder 25. Perzentil) ist die Zahl, die ein Viertel des geordneten Datensatzes markiert. Mit anderen Worten: Es gibt genau 25 % der Elemente, die unter dem ersten Quartilwert liegen, und genau 75 % der Elemente, die über diesem Wert liegen. Der Wert des ersten Quartils lässt sich leicht ermitteln, indem man die "mittlere" Zahl zwischen dem Minimum und dem Median findet. Bei den stündlichen Temperaturen liegt die "mittlere" Zahl zwischen 57 °F und 70 °F bei 66 °F. ⓘ

Der dritte Quartilswert (Q₃ oder 75. Perzentil) ist die Zahl, die drei Viertel des geordneten Datensatzes ausmacht. Mit anderen Worten: Genau 75 % der Elemente liegen unter dem dritten Quartil und 25 % der Elemente liegen darüber. Der Wert des dritten Quartils lässt sich leicht ermitteln, indem man die "mittlere" Zahl zwischen dem Median und dem Maximum sucht. Für die stündlichen Temperaturen ist die "mittlere" Zahl zwischen 70 °F und 81 °F 75 °F. ⓘ

Der Interquartilsbereich (IQR) kann berechnet werden, indem der erste Quartilswert (Q₁) vom dritten Quartilswert (Q₃) abgezogen wird:

${\text{IQR}}=Q_{3}-Q_{1}=75^{\circ }F-66^{\circ }F=9^{\circ }F.$ ⓘ

Daraus folgt, $1.5{\text{IQR}}=1.5\cdot 9^{\circ }F=13.5^{\circ }F.$ ⓘ

1,5 IQR oberhalb des dritten Quartils ist:

$Q_{3}+1.5{\text{ IQR}}=75^{\circ }F+13.5^{\circ }F=88.5^{\circ }F.$ ⓘ

1,5 IQR unterhalb des ersten Quartils ist:

$Q_{1}-1.5{\text{ IQR}}=66^{\circ }F-13.5^{\circ }F=52.5^{\circ }F.$ ⓘ

Die obere Whisker-Grenze des Box-Plots ist der größte Datenwert, der innerhalb von 1,5 IQR über dem dritten Quartil liegt. Hier liegt der 1,5 IQR über dem dritten Quartil bei 88,5 °F und der Höchstwert bei 81 °F. Daher wird der obere Whisker beim Wert des Maximums gezogen, der 81 °F beträgt. ⓘ

Analog dazu ist die untere Whisker-Grenze des Box-Plots der kleinste Datenwert, der innerhalb von 1,5 IQR unter dem ersten Quartil liegt. In diesem Fall ist 1,5 IQR unter dem ersten Quartil 52,5 °F und das Minimum ist 57 °F. Daher wird der untere Whisker beim Wert des Minimums gezogen, der 57 °F beträgt. ⓘ

Beispiel mit Ausreißern

Abbildung 6. Der generierte Boxplot für das Beispiel links mit Ausreißern. ⓘ

Oben sehen Sie ein Beispiel ohne Ausreißer. Hier ist ein Folgebeispiel für die Erstellung eines Boxplots mit Ausreißern: Die geordnete Menge für die aufgezeichneten Temperaturen ist (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89. ⓘ

In diesem Beispiel werden nur die erste und die letzte Zahl geändert. Der Median, das dritte Quartil und das erste Quartil bleiben gleich. ⓘ

In diesem Fall ist der Höchstwert in diesem Datensatz 89 °F, und 1,5 IQR über dem dritten Quartil ist 88,5 °F. Das Maximum ist größer als 1,5 IQR plus das dritte Quartil, also ist das Maximum ein Ausreißer. Daher wird der obere Whisker bei dem größten Wert gezogen, der kleiner als 1,5 IQR über dem dritten Quartil ist, d. h. bei 79 °F. ⓘ

In ähnlicher Weise beträgt der Mindestwert in diesem Datensatz 52 °F, und 1,5 IQR unter dem ersten Quartil ist 52,5 °F. Das Minimum ist kleiner als 1,5 IQR minus das erste Quartil, also ist das Minimum auch ein Ausreißer. Daher wird der untere Whisker bei dem kleinsten Wert gezogen, der größer als 1,5 IQR unter dem ersten Quartil ist, d. h. bei 57 °F. ⓘ

Im Falle großer Datensätze

Ein weiteres Beispiel für die Erstellung eines Box-Plots aus einem Datensatz mit einer großen Anzahl von Datenpunkten ist: ⓘ

Allgemeine Gleichung zur Berechnung der empirischen Quantile

$q_{n}(p)=x_{(k)}+\alpha (x_{(k+1)}-x_{(k)})$ ⓘ

${\text{with }}k=[p(n+1)]{\text{ and }}\alpha =p(n+1)-k$

Hier steht $x_{(k)}$ für die allgemeine Anordnung der Datenpunkte steht (d. h. wenn $i<k$, dann $x_{(i)}<x_{(k)}$ ) ⓘ

Anhand des obigen Beispiels mit 24 Datenpunkten (n = 24) kann man den Median, das erste und das dritte Quartil entweder mathematisch oder visuell berechnen. ⓘ

Median : $q_{n}(0.5)=x_{(12)}+(0.5\cdot 25-12)\cdot (x_{(13)}-x_{(12)})=70+(0.5\cdot 25-12)\cdot (70-70)=70^{\circ }F$ ⓘ

Erstes Quartil : $q_{n}(0.25)=x_{(6)}+(0.25\cdot 25-6)\cdot (x_{(7)}-x_{(6)})=66+(0.25\cdot 25-6)\cdot (66-66)=66^{\circ }F$ ⓘ

Drittes Quartil : $q_{n}(0.75)=x_{(18)}+(0.75\cdot 25-18)\cdot (x_{(19)}-x_{(18)})=75+(0.75\cdot 25-18)\cdot (75-75)=75^{\circ }F$ ⓘ

Visualisierung

Abbildung 7. Box-Plot und eine Wahrscheinlichkeitsdichtefunktion (pdf) einer normalen N(0,1σ²) Population ⓘ

Auch wenn Box-Plots primitiver erscheinen als Histogramme oder Kernel-Dichte-Schätzungen, haben sie doch eine Reihe von Vorteilen. Erstens können Statistiker mit Hilfe des Box-Plots eine schnelle grafische Untersuchung eines oder mehrerer Datensätze durchführen. Box-Plots benötigen auch weniger Platz und sind daher besonders nützlich, um Verteilungen zwischen mehreren Gruppen oder Datensätzen parallel zu vergleichen (siehe Abbildung 1 für ein Beispiel). Schließlich kann die Gesamtstruktur von Histogrammen und Kerndichteschätzungen durch die Wahl der Anzahl und Breite der Bins bzw. die Wahl der Bandbreite stark beeinflusst werden. ⓘ

Obwohl die Betrachtung einer statistischen Verteilung üblicher ist als die Betrachtung eines Boxplots, kann es nützlich sein, den Boxplot mit der Wahrscheinlichkeitsdichtefunktion (theoretisches Histogramm) für eine N(0,σ²)-Normalverteilung zu vergleichen und ihre Merkmale direkt zu beobachten (wie in Abbildung 7 dargestellt). ⓘ

Abbildung 8. Box-Plots zur Darstellung der Schiefe des Datensatzes ⓘ